AGRO SUR 33 (2) 49-61 2005
CIENCIA AGRARIA
ESTIMACIÓN DE LA EVAPOTRANSPIRACIÓN DE REFERENCIA EN LA LOCALIDAD DE REMEHUE-OSORNO, X REGIÓN
Estimation of Crop Reference Evapotranspiration for Remehue-Osorno, X Region
Fulvio Rivano G. 1 y Jorge Jara R. 2
1
Departamento de Recursos Hídricos, Facultad de Ingeniería Agrícola, Universidad
de Concepción. Casilla 537. Chillán, Chile. E-mail: frivano@udec.cl
2 Departamento de Recursos Hídricos, Facultad
de Ingeniería Agrícola, Universidad de Concepción. Casilla 537. Chillán,
Chile. E-mail: jcjara@udec.cl
ABSTRACT
In order to obtain reliable daily estimates of crop reference evapotranspiration (ET0) for Remehue-Osorno, a study was carried out to analyze four calculation procedures of daily mean vapor pressure deficit (VPD) and its impact on the Penman-Monteith (PM) ET0. Moreover, an adjustment of the Hargreaves-Samani (HS) equation coefficients was performed. Results indicated that the VPD procedure which makes use of maximum and minimum relative humidity associated with saturation vapor pressure at minimum and maximum air temperature, respectively, provides the most accurate VPD estimates with minimal effects on ET0 estimates. The locally adjusted HS equation that uses the observed solar radiation provides reliable and robust daily ET0 estimates similar to those obtained by the PM model. It was also found that previous studies on evapotranspiration for Remehue-Osorno would overpredict monthly ET0 estimates.
RESUMEN
Con el propósito de establecer estimaciones confiables de evapotranspiración de referencia (ET0) en la localidad de Remehue-Osorno, se realizó un estudio para analizar cuatro procedimientos de cálculo del déficit de presión de vapor (DPV) medio diario y su efecto en la estimación diaria de ET0 utilizando el modelo de Penman-Monteith (PM). Además, se realizó un ajuste de los coeficientes de la ecuación de Hargreaves-Samani (HS). Los resultados indican que el procedimiento de estimación del DPV que utiliza la humedad relativa máxima y mínima, asociada a la presión de saturación de vapor a la temperatura mínima y máxima del aire, respectivamente, simula mejor el DPV medio diario, con un efecto mínimo en la estimación de ET0. La ecuación de HS ajustada localmente, que utiliza la radiación solar observada, permite obtener estimaciones diarias de ET0 tan confiables y robustas como aquellas obtenidas con PM. Finalmente, estudios de evapotranspiración desarrollados con anterioridad para el sector de Remehue-Osorno presentarían valores sobrestimados de ET0 mensual.
Palabras clave: Evapotranspiración de referencia; Déficit de presión de vapor; Penman-Monteith; Hargreaves-Samani; Remehue; Osorno.
INTRODUCCIÓN
La creciente inversión en obras de negó y drenaje actualmente existente en la provincia de Osorno necesita de estimaciones confiables de los requerimientos de agua de aquellos cultivos tradicionales en esa zona. En el procedimiento clásico de estimación de la evapotranspiración de cultivo, el poder evaporativo de la atmósfera se cuantifica por la Evapotranspiración de referencia (ETref), mientras que las características de la superficie son incorporadas en un coeficiente de cultivo (Kc). La FAO y la ASCE han estandarizado el procedimiento de calculo de la ETref con el modelo de Penman-Monteith (PM) para un cultivo corto semejante al pasto (ET0) (Allen et al., 1998) y luego para un cultivo largo similar a la alfalfa (ETr) (ASCE EWRI 2005). Sin embargo, no existe consenso respecto de una metodología única para determinar el déficit de presión de vapor (DPV) medio diario Recientemente, Irmak et al. (2006) develaron una alta sensibilidad de ETref respecto del DPV en diferentes condiciones climáticas de EE.UU. Así, un error en la forma de calculo del DPV medio diario puede ser transmitido a la estimación de ETref.Parte del problema proviene de las variadas formas en la cual se mide y reporta la humedad atmosférica, y el álgebra utilizada en el calculo el DPV medio diario. Sadler y Evans (1989), al comparar 15 métodos de calculo del DPV medio diario, reportaron diferencias de -80 a +100% en las estimaciones de ET0 en una amplia variedad de ambientes. De igual forma, Howell y Dusek (1995), al investigar la precisión de 5 métodos de calculo del DPV medio diario, documentaron errores de hasta un 25% en Texas, aunque no investigaron la propagación del error en la estimación de ET0.
La cantidad de variables meteorológicas requeridas por el modelo de PM y la escasa disponibilidad de estaciones meteorológicas con condiciones de referencia y registros confiables, ha motivado el desarrollo de modelos empíricos mas simples como el de Hargreaves y Samani (HS) (1985). Muchos estudios han mostrado que el modelo de HS provee estimaciones confiables de ET0 para tiempos de resolución mayores a cinco días (Hargreaves, 1989; Hargreaves, 1994; Jensen et al., 1997; Droogers y Allen, 2002; Hargreaves y Allen, 2003), y se conoce su tendencia a sobrestimar ET0 en climas húmedos (Jensen et al., 1990; Itenfisu et al., 2003; Temesgen et al., 2005; Trajkovic, 2005). En consecuencia, muchos estudios se han dirigido a mejorar la calidad de las estimaciones realizando calibraciones locales o regionales de los coeficientes originales en diferentes condiciones climáticas (Martínez-Cob y Tejero-Juste 2004; Vanderlinden et al., 2004; Gavilan et al., 2006; Mercado, 2006; Trajkovic, 2007; Vega, 2007).
Hasta la fecha, en Remehue-Osorno, no existen estudios de validación de ETref, y aquellos desarrollados con fines de diseño (MOP 1990; Valenzuela, 1990; CIREN-CNR, 1997) no definen las características del cultivo de referencia ni precisan la metodología empleada en la obtención de las variables utilizadas El presente trabajo tiene como objetivo (1) comparar distintos procedimientos de calculo del DPV medio diario y evaluar su efecto en la estimación diana de ET0 en la localidad de Remehue, y (2) determinar los coeficientes de la ecuación de HS para estimaciones dianas de ET0.
MATERIALES Y MÉTODO
Recolección de Datos Meteorológicos
Los datos utilizados en este estudio fueron recolectados por la estación meteorológica del Centro Regional de Investigación INIA-Remehue (40°35' S, 73°08' W, 73 m.s.n.m ). De los 30 años actualmente registrados por la estación, 3176 días comprendidos entre Julio de 1989 y Junio de 1998, fueron seleccionados para el presente estudio por poseer información completa de la humedad relativa máxima y mínima temperatura máxima y mínima, velocidad de viento y radiación solar Los instrumentos empleados en la obtención de la variables meteorológicas fueron psicrómetro (R. Fuess modelo August), termómetros ambientales (R. Fuess), veleta anemométrica (R. Fuess modelo Wild) y actinógrafo (R. Fuess modelo 58 DC).
El Centro Regional de Investigación INIA-Remehue presenta un clima mediterráneo frío que, según Novoa y Villaseca (1989), se caracteriza por presentar una temperatura media anual de 11,4 °C, con una máxima media del mes más cálido (enero) de 23,8 °C y una mínima media del mes más frío (junio) de 3,2 °C. La precipitación media anual es de 1.383 mm., siendo mayo el mes más lluvioso con 253,7 mm y febrero el único mes seco, con 50 mm.
Determinación de la Evapotranspiración de Referencia
La ET0 ha sido definida por Allen et al. (1998) y la ASCE-EWRI (2005) como la evapotranspiración de un cultivo hipotético de 0,12 m de altura, con albedo de 0,23 y resistencia de cultivo de 70 s m-1 (para intervalos de tiempo diarios), determinada por el método de PM. Para intervalos de tiempo menores, ciertas variaciones han sido incorporadas (Allen et al., 2006). La ecuación de PM es un modelo físicamente basado y para intervalos de tiempo diarios tiene la siguiente forma:
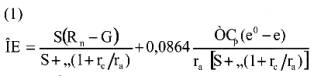
donde λE es el flujo de calor latente (MJ m-2 d-1), S es la pendiente de la curva de saturación de vapor (kPa °C-1), Rn es la radiación neta (MJ m-2 d-1), G es la densidad de flujo de calor del suelo (MJ m-2 d-1), r es la densidad del aire (kg m-3), C es el calor específico del aire húmedo (1013 J kg-1 °C-1), (e0-e) es el DPV medio diario (kPa), ra es la resistencia aerodinámica (s m-1), rc es la resistencia del cultivo (70 s m-1) y g es la constante psicrométrica (kPa °C-1).
En estimaciones diarias, la densidad de flujo de calor del suelo puede ser despreciada y Rn puede estimarse como:
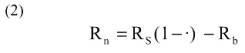
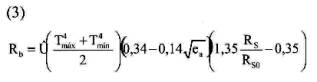
donde σ es la constante de Stefan-Boltzmann (4,903∞ 10-9 MJ m-2 d-1 K-4),Tmáx y Tmín son la temperatura máxima y mínima diaria (K), respectivamente; ea es la presión de vapor media diaria (kPa) y RS0 es la radiación solar a nivel de suelo en un día despejado (MJ m-2 d-1).
La presión de vapor media diaria es estimada por la siguiente expresión sugerida por Allen et al. (1998):
![]()
donde e0(Tmín) es la presión de saturación de vapor a la temperatura mínima diaria (kPa), y HRmáx es la humedad relativa máxima diaria.
Cuando no existen datos calibrados, RS0 puede ser estimada a partir de:
![]()
donde z es la altitud de la estación y Ra es la radiación extraterrestre (MJ m-2 d-1) estimada por el procedimiento estándar presentado por Allen et al. (1998) y la ASCE-EWRI (2005).
Por otra parte, la resistencia aerodinámica es expresada como:
(6)
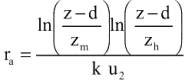
donde z es la altura de medición estándar de la velocidad del viento (2 m), d es la altura del plano de desplazamiento cero del cultivo de referencia (0,08 m), zm y zh son el parámetro de rugosidad para la transferencia de momentum (0,01476 m) y el parámetro de rugosidad de para la transferencia de vapor y calor (2,952∞ 10-3 m), respectivamente, k es la constante de von Karman (0,41) y u2 es la velocidad del viento (m s-1) medida a 2 m. Puesto que el viento fue medido a 5 m de altura, su velocidad fue convertida a una equivalente de 2 m de altura usando la siguiente ecuación propuesta por Allen et al. (1998):
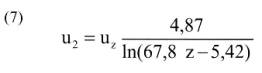
donde uz es la velocidad del viento medida a la altura z (m).
La pendiente de la curva de saturación (kPa °C-1) utilizada fue:
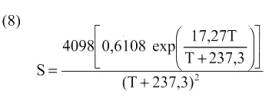
donde T es la temperatura media diaria (°C). La siguiente expresión fue utilizada para estimar la constante psicrométrica (kPa °C-1):
![]()
donde P es la presión atmosférica (kPa).
La densidad del aire (kg m-3) se estimó utilizando la expresión sugerida por Shuttleworth (1993):
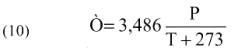
donde P es la presión atmosférica (kPa) y T es la temperatura media diaria (°C).
En ausencia de un registro continuo, el DPV en cada hora sinóptica (08:00, 14:00 y 20:00) fue utilizado para entregar el DPV medio diario (DPVprom) con el cual se comparó la ET0.
obtenida con otros procedimientos de estimación de DPV comúnmente utilizados y recomendados. El DPV es definido como

donde el subíndice denota la hora sinóptica.
El primer procedimiento de estimación del DPV medio diario considera el déficit de presión de vapor máximo y mínimo calculado en horas sinópticas (método 12 de Sadler y Evans, 1989):

El segundo procedimiento de estimación del DPV medio diario utiliza la presión de saturación de vapor a la temperatura máxima, mínima y la humedad relativa máxima (Ecs. (12) y (18) de Allen et al., 1998; Ecs. (6) y (12) de la ASCE-EWRI, 2005):

donde la presión de saturación de vapor a la temperatura de punto de rocío es estimada con la ecuación (4).
El tercer procedimiento de estimación del DPV medio diario utiliza la presión de saturación de vapor a la temperatura media diaria e0(T) , y la humedad relativa máxima y mínima (Método I de Doorenbos y Pruitt, 1977)
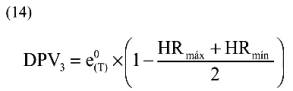
El cuarto procedimiento de estimación del DPV medio diario utiliza la presión de saturación de vapor a la temperatura máxima y mínima, asociada a la humedad relativa mínima y máxima (Método IV de Doorenbos y Pruitt, 1977; Ecs. (12) y (17) de Allen et al., 1998; Ecs. (6) y (11) de la ASCE-EWRI, 2005):
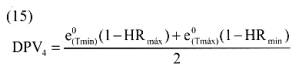
Ecuación de Hargreaves-Samani
La ecuación de HS ha sido ampliamente usada y estudiada en la última década debido a su simplicidad, confiabilidad, mínimos requerimientos climáticos, facilidad de computación y bajo impacto en ambientes altamente advectivos. Esta ecuación utiliza solamente datos de temperatura y su forma original es:
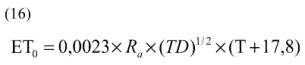
donde ET0 es la evapotranspiración de referencia (mm d-1), TD es la diferencia entre la temperatura máxima y mínima diaria (°C), T es la temperatura media diaria (°C) y Ra es la radiación extraterrestre (mm d-1). Hargreaves y Samani (1982; 1985) desarrollaron esta ecuación desde dos ecuaciones independientes; la primera relaciona la radiación solar (RS) y T con ET0:
![]()
donde KE es un coeficiente de calibración (originalmente 0,0135) y RS está en unidades de evapotranspiración (mm d-1). La segunda ecuación es un modelo radiactivo que relaciona Ra y TD con RS:
![]()
donde KT es un coeficiente de calibración. Hargreaves et al. (1985) calibraron esta ecuación utilizando datos de la cuenca del río Senegal y Mali, y encontraron un valor de KT de 0,16. Combinando las ecuaciones (17) y (18) Hargreaves et al. (1985) obtuvieron la ecuación (16) con un coeficiente de 0,0022 desde un promedio de 82 estaciones en Africa y 62 estaciones en Brasil, y un valor de 0,0023 en Davis. California (EE.UU.). Sin embargo, Samani y Pessarakli (1986) reportaron valores de KT que fluctúan entre 0,119 y 0,212 en diferentes localidades de EE.UU. Finalmente la ecuación (16) se aceptó para uso general sin mayor calibración.
En el presente estudio se analizaron cuatro variantes de la ecuación de HS:
• HSorig,RSO: ecuación (17) con KE = 0,0135 y la radiación solar es la observada (RSO).
• HScalib,RSE: ecuación (17) con KE ajustado localmente y la radiación solar es estimada (RSE) por la ecuación (18) con KT ajustado localmente.
• HScalib,RSO: ecuación (17) con KE ajustado localmente y la radiación solar es RSO.
De los 3176 días disponibles para el análisis, 1415 días comprendidos entre julio de 1989 y junio de 1993 fueron utilizados para el ajuste de los coeficientes de la ecuación, mientras que los restantes 1761 días, correspondientes al período de julio de 1993 a junio de 1998 fueron utilizados para validar la calidad de las estimaciones.
Los coeficientes KE y KT fueron calculados por mínimos cuadrados ordinarios en forma independiente, utilizando los registros diarios de RS, temperatura media, mínima y máxima, mientras que ET0 se estimó con el modelo de PM utilizando el DPVprom. La Ra se estimó según el procedimiento estándar presentado por Allen et al. (1998) y la ASCE-EWRT (2005).
Comparación y Evaluación de Estimaciones
La ET0 calculada con el método de PM y el DPVprom de la ecuación (11), se establecieron como base de comparación en la evaluación de los otros métodos de estimación de ET0 y DPV. La bondad de cada modelo se evaluó utilizando los criterios de raíz del error cuadrático medio (RMSE), error absoluto medio (MAE), coeficiente de eficiencia modificado por Legales y McCabe (1999) (E1) y cociente medio (MR):
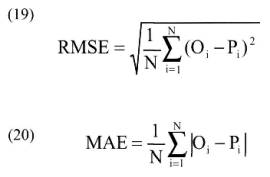
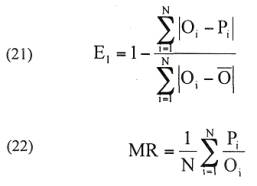
donde O son datos de referencia, P son datos estimados, y N es el número de comparaciones realizadas.
RESULTADOS Y DISCUSIÓN
Procedimientos de Cálculo del DPV y su Impacto en la Estimación de ET0
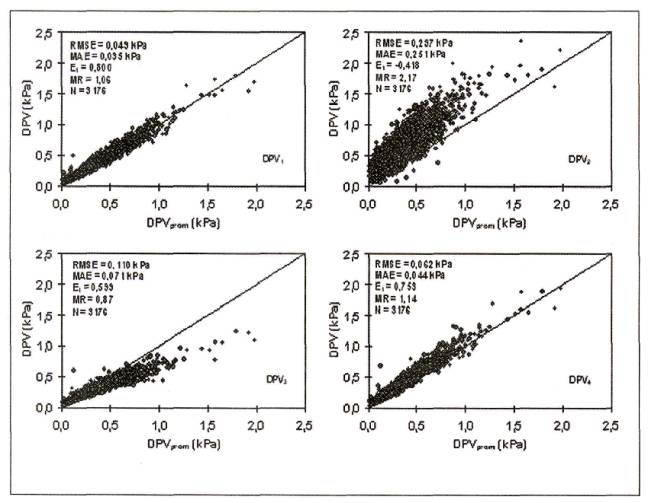
Es posible apreciar que las estimaciones del DPV1 y DPV4 simulan satisfactoriamente aquellas del DPVprom, con valores de RMSE y MAE menores a 0,062 kPa, y E, y MR cercanos a la unidad (Figura 1). Al igual que con la temperatura, el promedio de los valores del DPV máximo y mínimo diario es un buen estimador del DPV medio diario, con la salvedad que los valores de DPV máximo y mínimo fueron calculados en horas sinópticas y no representan el verdadero DPV máximo o mínimo diario. Por el contrario, el estimador DPV4 logra un desempeño similar haciendo uso de parámetros meteorológicos más fáciles de obtener. Estimaciones del DPV3, con valores de RMSE y MAE de 0,11 y 0,071 kPa, respectivamente, subestiman aquellas del DPVprom en 13%, mientras que estimaciones del DPV2, sobrestiman los valores del DPVprom en 117%, con valores de RMSE y MAE de 0,297 y 0,251 kPa, respectivamente.
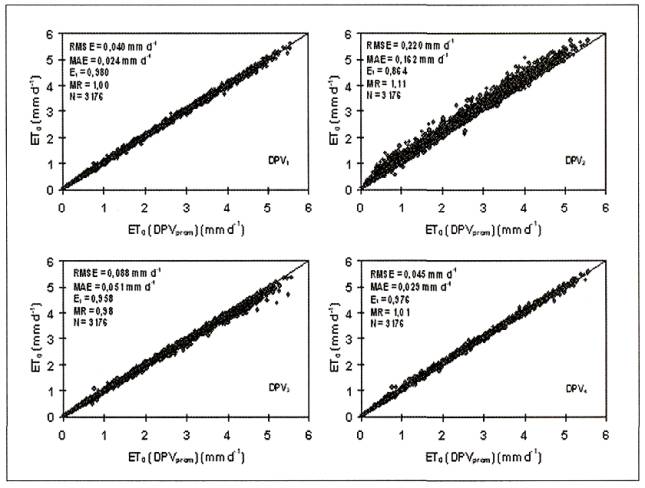
Puesto que el DPV es un indicador de la actual demanda evaporativa del aire, la diferencia entre la ET0 estimada con distintos procedimientos de cálculo del DPV y la ET0 estimada con el DPVprom tiene un comportamiento similar a las diferencias entre procedimientos de cálculo del DPV de la Figura 1, pero atenuadas por el parámetro de la energía disponible para el proceso de evapotranspiración, tal como se aprecia en la Figura 2. Así, el DPV1, y el DPV4, que fueron los mejores estimadores del DPV medio diario, presentan valores de ET0 con RMSE y MAE menores a 0,05 mm d-1, y E1, y MR cercanos a la unidad. Estos resultados concuerdan con aquellos presentados por Yoder et al. (2005), quienes en la meseta húmeda de Cumberland, Tennessee (EE.UU.), encontraron que el DPV4 era el mejor estimador del DPV medio diario. Sin embargo, este procedimiento de calculo resulto ser el peor evaluado por Howell y Dusek (1995) en las condiciones semiáridas de las planicies altas del sur de Texas (EE.UU.). En consecuencia, pareciera que el DPV4 es un buen estimador del DPV medio diario en climas húmedos, aunque una explicación teórica resulta compleja debido a la dependencia del DPV con la distribución diana de la temperatura y la presión de vapor Finalmente, valores de ET0 calculados con DPV3 subestiman levemente a aquellos de ET0 (DPVprom), y aquellos obtenidos con DPV2 resultan inapropiados puesto que sobrestiman en 11 % los valores de ET0 (DPVrom) con RMSE y MAE de 0,22 y 0,162 mm d-1, respectivamente, resultando en un estimador sesgado del DPV para las condiciones climáticas de la zona en estudio.
Ecuación de Hargreaves-Samani
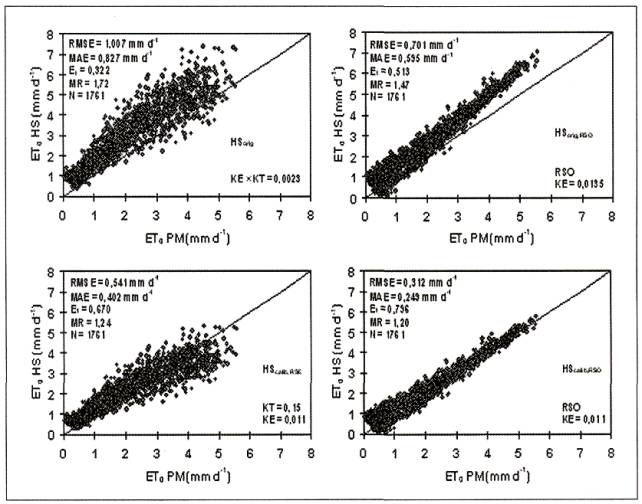
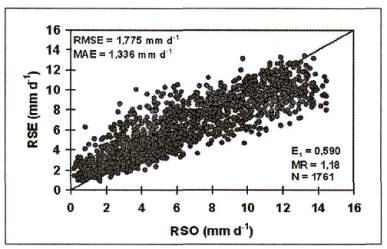
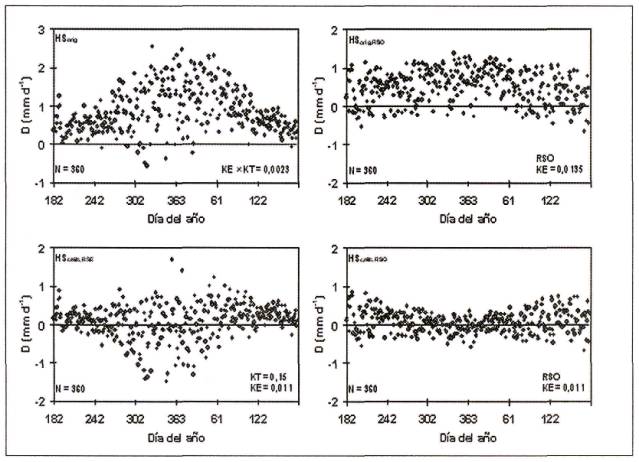
La Figura 3 presenta las estimaciones dianas de ET0 desde las cuatro variantes de la ecuación de HS versus ET0 estimada con PM. Es posible apreciar que la ecuación de HS original, con coeficientes no ajustados, sobrestima la ET0 con valores de RMSE de 1,007 y 0,701 mm d-1 y MAE de 0,827 y 0,595 mm d-1, cuando se utilizo el modelo radiativo (HSorig) o RSO (HSorig,RSO), respectivamente. El ajuste local de la ecuación de HS (HScalib,RSE y HScalib,RSO), reduce los valores de RMSE a 0,541 y 0,312 mm d-1, y MAE a 0,412 y 0,249 mm d-1, respectivamente. En consecuencia, al utilizar RSO en vez de RSE (modelo radiativo), la calidad de predicción de ET0 mejora en 30% para el caso de la ecuación de HS original y en un 40% para la ecuación de HS ajustada. La Figura 4 presenta la validación del ajuste local del modelo radiativo, que presenta valores de RMSE y MAE de 1,775 y 1,336 mm d-1, equivalentes a 4,349 y 3,273 MJ m-2 d-1, respectivamente. Estos valores son similares e incluso menores a los reportados por Hunt et al. (1998), Weiss et al. (2001) y Ball et al. (2004), en ciertas localidades de Canadá y EE.UU., utilizando los modelos de Hunt, HS, Weiss, Bristow-Campbell y modificaciones de ellos. No obstante, aun con una buena calidad predictiva, el patrón de dispersión del modelo radiativo se manifiesta en la ecuación ajustada de HS (HScalib,RSE), reduciendo su bondad de ajuste para estimaciones diarias de ET0.
El valor del coeficiente KT presentado en el Cuadro 1 es similar al obtenido en EE.UU. por Samani y Pessarakli (1986) en las localidades de Montgomery, Alabama (0,149), Bismarck, North Dakota (0,150) y Detroit, Michigan (0,149) por Samani (2000) en la localidad de Portland, Maine (0,150), y por Mercado (2006) en la localidad de Chillán (0,150). En general, este valor es menor a 0,16, obtenido por Hargreaves et al (1985), e indica la sobrestimación que presenta el modelo radiativo original. De igual forma, el valor del coeficiente KE es menor a 0,0135, presentado originalmente por Hargreaves (1975), y a 0,0162, indicado por Samani y Pessarakli (1986). Recientemente, Mercado (2006), en Chile, y Vega (2007), en Ecuador, reportaron bajos valores de KE (0,012 en Chillán y 0,008 en Portoviejo). En consecuencia, el valor de KE podría ser indicativo de la aridez o humedad de un sector, siendo valores bajos característicos de zonas húmedas.
 |
| SD: desviación estándar R2: coeficiente de determinación |
Con el objeto de identificar la distribución estacional de las diferencias en la estimación de ET0 de las cuatro variantes de la ecuación de HS con PM, se evaluó el periodo comprendido entre julio de 1994 y junio de 1995 (Figura 5). Es posible observar que, en general, la ecuación de HS no ajustada tiende a sobrestimar la ET0 a lo largo del año Cuando esta ecuación incorpora el modelo radiativo, se presenta una gran dispersión en los meses de verano, que es cuando se requiere de mayor precisión en las estimaciones de ET0. No obstante, en ese periodo, la ecuación ajustada que utiliza la radiación solar observada presenta diferencias inferiores a los ±0,5 mm d-1, indicando que es un método altamente confiable para estimaciones dianas de ET0. En consecuencia, futuros estudios de ET0 en esta zona debieran dirigir su atención hacia la formulación o calibración de un modelo radiativo mas preciso, que permita reducir la actual dispersión en las diferencias de ET0 entre HScalib,RSE y PM.
Comparación de Estudios de Evapotranspiración de Referencia
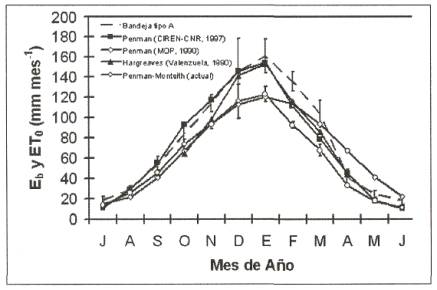
La Figura 6 presenta las estimaciones promedio mensuales de ET0 desarrolladas para la localidad de Remehue-Osorno por el MOP (1990), Valenzuela (1990) y CIREN-CNR (1997), con aquellas calculadas con PM (utilizando el DPVprom) estimadas como el promedio de los totales mensuales de la ET0 diaria en los meses con registros diarios completos. En diciembre y enero, la ET0 determinada por Valenzuela (1990), con el método de Hargreaves, y aquella determinada por CIREN-CNR (1997), con el método de Penman, sobrestiman en unos 30 mm mes-1 la ET0 estimada con PM, con valores similares a la evaporación de bandeja promedio del período en estudio. Las estimaciones de ET0 determinadas por el MOP (1990), con el método de Penman, son muy similares a las obtenidas con PM desde julio a enero; sin embargo, de febrero a junio hay una sobrestimación de 25 mm mes-1 utilizando el método de Penman. En general, es posible observar que los estudios de ET0 desarrollados hasta la fecha muestran una tendencia a la sobrestimación en algún período del año. En consecuencia, su utilización con fines de manejo y conservación del agua, producción agrícola o evaluación ambiental podría resultar cuestionable.
CONCLUSIONES
Los mejores procedimientos de estimación del DPV medio diario para la zona Remehue-Osorno son el que utiliza el DPV máximo y mínimo medido en horas sinópticas (DPV1) y aquel que utiliza la presión de saturación de vapor a la temperatura máxima y mínima y la humedad relativa máxima y mínima (DPV4). No obstante, este último procedimiento utiliza información meteorológica que es más fácil de obtener por lo que se recomienda su uso. El método que utiliza la presión de saturación de vapor a la temperatura máxima, mínima y la humedad relativa máxima (DPV2), es el menos adecuado por cuanto sobrestima el DPV medio diario en 117%.
Al evaluar el efecto de los cuatro diferentes métodos de cálculo del DPV en la estimación de ET0, se encontró que los métodos DPV1 y DPV4 producían mínimas alteraciones en la estimación de ET0.
El mejor ajuste de la ecuación de HS para el sector de Remehue-Osorno arrojó valores de los coeficientes KT y KE de 0,150 y 0,0110, respectivamente. No obstante, al utilizar la RSO en vez de la RSE, se mejora la calidad de la predicción en un 40%, resultando en una alternativa simple y robusta de estimación diana de ET0. Aún cuando el modelo radiativo ajustado presenta indicadores estadísticos comparables a los presentados por otros estudios en algunas localidades de EE.UU. y Canadá, su patrón de dispersión se transfiere a la estimación de ET0, por lo que se advierte la necesidad de formular y/o calibrar modelos radiativos más precisos para la zona.
Estudios previos de ET0 desarrollados para el sector de Remehue-Osorno presentarían valores sobrestimados de ET0 mensual en algún período del año, lo que debiera ser considerado para fines de planificación, diseño, manejo y conservación del agua.
AGRADECIMIENTOS
Los autores desean agradecer la información meteorológica proporcionada por los Sres. Rene Bernier y Aldo Valdebenito del Centro Regional de Investigación INIA-Remehue.
BIBLIOGRAFÍA
ALLEN, R.G.; PEREIRA, L.S.; RAES, D.; SMITH, M. 1998. Crop evapotranspiration, guidelines for computing crop water requirements. FAO Irrigation and Drainage Paper 56. Food and Agriculture Organization. Roma.
ALLEN, R.G.; PRUITT, W.O.; WRIGHT, J.L.; HOWELL, T.A.; VENTURA, F.; SNYDER, R.; ITENFISU, D.; STEDUTO, P.; BERENGENA, J.; YRISARRY. J.B.; SMITH, M.; PEREIRA, L.S.; RAES, D.; PERRIER, A.; ALVES, I.; WALTER, I.; ELLIOTT, R. 2006. A recommendation on standardized surface resistance for hourly calculation of reference ET0 by FAO56 Penman Monteith method. Agric. Water Manage 81(1-2), 1-22.
ASCE-EWRI. 2005. The ASCE standardized reference crop evapotranspiration equation Technical Committee Report on Environmental and Water Resource Institute of the American Society of Civil Engineers from the Task Committee on Standardization of Reference Evapotranspiration. Reston, VA.
BALL, R.A.; PURCELL, L.C.; CAREY, S.K. 2004. Evaluation of solar radiation prediction models in North America. Agron. J. 96, 391-397.
CIREN-CNR. 1997. Calculo y cartografía de la evapotranspiración potencial en Chile. Centro de Información de Recursos Naturales y Comisión Nacional de Riego. Santiago.
DOORENBOS, J.; PRUITT, W.O. 1977. Guidelines for predicting crop water requirements. FAO Irrigation and Drainage Paper 24. Food and Agriculture Organization. Roma.
DROOGERS, P.; ALLEN, R.G. 2002. Estimating reference evapotranspiration under inaccurate data conditions. Irrig. Dram. Syst. 16, 33-45.
GAVILAN, P.; LORITE, I.J.; TORNERO, S.; BERENGENA, J. 2006. Regional calibration of Hargreaves equation for estimating reference ET in a semiarid environment. Agric. Water Manage. 81, 257-281.
HARGREAVES, G.H. 1975. Moisture availability and crop production. Trans ASAE 18(5), 980-984.
HARGREAVES, G.H. 1989. Accuracy of estimated reference crop evapotranspiration. J. Irrig. Dram. Eng. 115(6), 1000-1007.
HARGREAVES, G.H. 1994. Defining and using reference evapotranspiration. J. Irrig. Dram. Eng. 120(6), 1132-1139.
HARGREAVES, G.H.; ALLEN, R.G. 2003. History and evaluation of Hargreaves evapotranspiration equation. J. Irrig. Dram. Eng. 129(1), 53-63.
HARGREAVES, G.L.; HARGREAVES, G.H.; RILEY, J.P. 1985. Irrigation water requirements for Senegal river basin. J. Irrig. Dram. Eng. 111(3), 265-275.
HARGREAVES, G.H.; SAMANI, Z.A. 1982. Estimating potential evapotranspiration. J. Irrig. Dram. Div. Proc. ASCE 108 (IR3), 225-230.
HARGREAVES, G.H.; SAMANI, Z.A. 1985. Reference crop evapotranspiration from temperature. Appl. Eng. Agric. 1(2), 96-99.
HOWELL, T.A.; DUSEK, D.A. 1995. Comparison of vapor pressure deficit calculation methods-southern high plains. J. Irrig. Dram. Eng. 121(2), 191-198.
HUNT, L.A.; KUCHAR, L.; SWANTON, C.J. 1998. Estimation of solar radiation for use m crop modelling. Agric. For. Meteorol. 91, 293-300.
ITENFISU, D.; ELLIOTTR. L.; ALLEN, R.G.; WALTER, I.A. 2003. Comparison of reference evapotranspiration calculations as part of the ASCE standardization effort. J. Irrig. Drain. Eng. 129(6), 440-448.
JENSEN. D.T.; HARGREAVES, G.H.; TEMESGEN, B.; ALLEN, R.G. 1997. Computation of ET0 under nonideal conditions. J. Irrig. Drain. Eng. 123(5), 394-400.
JENSEN, M.T.; BURMAN, R.D.; ALLEN, R.G. (eds.). 1990. Evapotranspiration and irrigation water requirements. ASCE Manuals and Reports on Engineering Practico 70. American Society of Civil Engineers. New York.
LEGATES, D.R.; McCABE, G.J. 1999. Evaluating the use of «goodness-of-fit» measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 35(1), 233-241.
MARTINEZ-COB, A.; TEJERO-JUSTE, M. 2004. A wind-based qualitative calibration of the Hargreaves ET0 estimation equation in semiarid regions. Agric. Water Manage. 54, 251-264.
MERCADO, G.H. 2006. Estimación de la evapotranspiración de referencia utilizando datos de temperatura del aire. Tesis MSc. Departamento de Recursos Hídricos, Universidad de Concepción. Chillán.
MOP. 1990. Investigación de riego y drenaje en la X Región. Dirección de Riego, Ministerio de Obras Públicas y R & Q Ingeniería Ltda. Santiago.
NOVOA, R.; VILLASECA, S. (eds.). 1989. Mapa agroclimático de Chile. Instituto de Investigaciones Agropecuarias. Santiago.
SADLER, E.J.; EVANS, D.E. 1989. Vapour pressure deficit calculations and their effect on the combination equation. Agric. For. Meteorol. 49, 55-80.
SAMANI, Z.A. 2000. Estimating solar radiation and evapotranspiration using minimum climatological data. J. Irrig. Drain. Eng. 126(4), 265-267.
SAMANI, Z.A.; PESSARAKLI, M. 1986. Estimating potential crop evapotranspiration with minimum data in Arizona. Trans. ASAE 29(2), 522-524.
SHUTTLEWORTH, W,J. 1993. Evaporation. In: D.R. Maidment (ed.) Handbook of Hydrology. McGraw-Hill, New York.
TEMESGEN, B.; ECHING, S.; DAVIDOFF, B.; FRAME, K. 2005. Comparison of some reference evapotranspiration equations for California. J. Irrig. Drain. Eng. 131(1), 73-84.
TRAJKOVIC, S. 2005. Temperature-based approaches for estimating reference evapotranspiration. J. Irrig. Drain. Eng. 131(4), 316-323.
TRAJKOVIC, S. 2007. Hargreaves versus Penman-Monteith under humid conditions. J. Irrig. Drain. Eng. 133(1), 38-42.
VALENZUELA, A. 1990. Requerimiento de riego de la zona sur del país. Departamento de Ingeniería Agrícola, Universidad de Concepción. Boletín de Extensión 44. Chillán.
VANDERLINDEN, K.; GIRALDEZ, J.V.; MEIRVENNE, V. 2004. Assessing reference evapotranspiration by the Hargreaves method in southern Spain. J. Irrig. Drain. Eng. 130(1), 184-191.
VEGA, E. 2007. Estimación de la evapotranspiración de referencia para dos zonas (costa y región andina) del Ecuador. Tesis MSc. Departamento de Recursos Hídricos, Universidad de Concepción. Chillán (en prensa).
WEISS, A.; HAYS, C.J.; HU, Q.; EASTERLING, W.E. 2001. Incorporating bias error in calculating solar irradiance: implications for crop yield simulations. Agron. J. 93, 1321-1326.
YODER, R.E.; ODHIAMBO. L.O.; WRIGHT, W.C. 2005. Effects of vapor-pressure deficit and net-irradiance calculation methods on accuracy of standardized Penman-Monteith equation in a humid climate. J. Irrig. Drain. Eng. 131(3), 228-237.
Recepción de originales: 23 de febrero de 2006