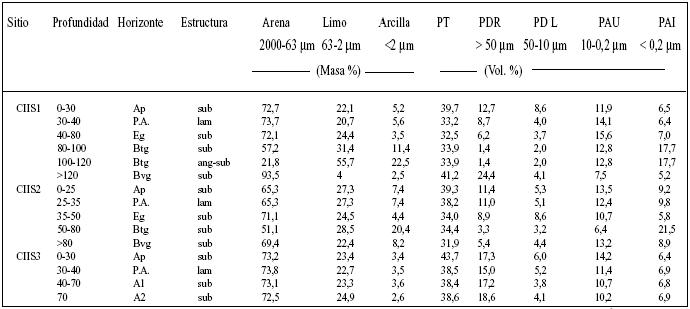
PA: Pie de arado; sub: bloque subangular; lam: laminar, ang: bloque angular
AGRO SUR 36(2) 93-100 2008
DOI:10.4206/agrosur.2008.v36n2-05
CIENCIA DEL SUELO
EFECTO DE LA ESTRUCTURA SOBRE EL MOVIMIENTO DE AGUA EN UNA CATENA DE SUELOS
José Dörner y Dorota Dec
Instituto de Ingeniería Agraria y Suelos Facultad Ciencias Agrarias, Universidad Austral de Chile e-mail: josedorner@uach.cl.
ABSTRACT
In order to describe the water flow in a soil catena, undisturbed
soil samples (vertical and horizontal with respect to the soil surface) were
collected in different soil areas and positions of a typical soil catena of
the Weichselian moraine region in Northern Germany. The water retention curve
and the saturated hydraulic conductivity (kf) were determined. The
water flow in the hill slope was simulated considering rainfall, evapotranspiration
and the hydraulic properties of the soil horizons.
Hydraulic conductivity was strongly related to the soil structure, the volume
of macropores, the interconnection and continuity between pores. The formation
of a plate structure in the plough pan leads to anisotropy of saturated hydraulic
conductivity (kf-H > kf-V) which can conduct a preferential
flow in the catena as represented in the simulation.
RESUMEN
Con el objetivo de describir el movimiento de agua en una catena de suelos, se recolectaron muestras no disturbadas (verticales y horizontales con respecto a la superficie del suelo) en los distintos horizontes y posiciones de una catena típica del paisaje de morrenas del Norte de Alemania. Se determinó la curva de retención de agua y la conductividad hidráulica en fase saturada (kf). Se modeló el movimiento de agua en la pendiente considerando las precipitaciones, evapotranspiración y las propiedades hidráulicas del suelo.
Se determinó que la conductividad hidráulica esta fuertemente ligada a la estructura del suelo, al volumen de macroporos y a la interconexión y continuidad entre ellos. La formación de estructura laminar en el pie de arado induce anisotropía en la conductividad hidráulica saturada (kf-H > kf-V) lo que puede generar un flujo preferencial de agua en la catena tal como se representa en la simulación.
Palabras claves: Movimiento de agua, conductividad hidráulica saturada, anisotropía.
INTRODUCCION
El suelo es un medio poroso en donde se produce el almacenamiento y transporte de agua, aire y calor. Estos procesos están estrechamente ligados a la textura y estructura del suelo. La estructura por un lado es función de la textura y del contenido de materia orgánica del suelo, pero por otro lado depende de la actividad biológica, de los ciclos de mojado y secado del suelo y del manejo que se ejerce sobre el recurso (Hartge y Horn, 1999).
La estructura del suelo juega un rol importante no tan sólo en el monto y la distribución del espacio poroso (Horn y Smucker, 2005) sino que también en la capacidad de suelo para transmitir agua (Ellies et al., 1997) y aire (Dörner y Dec, 2007). Ya que la estructura de un suelo puede presentar formas definidas, como por ejemplo un eje vertical mayor al horizontal (estructura columnar), es que la conductividad hidráulica saturada (kf) puede presentar anisotropía (en el caso de estructura columnar: kf-Vertical > kf-Horizontal). El comportamiento anisotrópico depende de la escala, es decir, podemos encontrar anisotropía en la escala del perfil y/o en la escala del horizonte de suelo, lo que se debe a que el suelo presenta heterogeneidades a distintas escalas, o sea, encontraremos distintos valores de conductividad asociados a dichas escalas (Youngs, 1991). Se ha establecido que suelos estratificados (por ejemplo suelos arenosos) presentan una componente horizontal de la conductividad hidráulica mayor que la vertical (Zaslavsky y Rogowski, 1969, Mualem, 1984). En ese caso el volumen total del suelo presenta anisotropía. También se ha observado dependencia espacial en horizontes individuales de suelo, como lo hicieron Hartge (1984) en un Luvisol bien estructurado, Dabney y Selim (1987) en un fragipán y Fazekas (2005) en suelos con dominancia de bioporos. En todos esos casos la componente vertical de la conductividad hidráulica era mayor que la horizontal.
El movimiento de agua en el suelo ocurre a través del medio poroso en más de una dimensión. Actualmente existen herramientas como la modelación que permiten simular la realidad y crear posibles escenarios para prevenir determinadas situaciones que pueden constituir un riesgo, como por ejemplo la contaminación de agua subterránea, el escurrimiento superficial de agua y la erosión, etc. Dichos modelos permiten la modelación del transporte de agua en una (movimiento de agua en una columna de suelo) y dos (movimiento de agua en una pendiente) dimensiones. En muchos de estos modelos se asume que la conductividad hidráulica es isotrópica, a pesar que varios autores han confirmado lo contrario (Mualem, 1984; Hartge, 1984; Fazekas, 2005). Considerar que kf presenta un comportamiento isotrópico permite una solución simple de la ecuación de Richards (base para modelación de los procesos de transporte), lo que, sin embargo, puede significar una subestimación del movimiento lateral de agua en una pendiente, ya que bajo dichas condiciones se asume que la dirección del flujo del agua es inverso al de la gradiente hidráulica sin que se produzca una desviación del flujo como consecuencia de la dependencia espacial de kf (Bear et al., 1987).
El objetivo de este trabajo fue presentar el efecto de la estructura del suelo sobre la dependencia espacial de la conductividad hidráulica en fase saturada y sobre el transporte de agua en una catena de suelos.
MATERIAL Y METODO
Suelos y manejo
Los suelos estudiados corresponden a una secuencia de Luvisoles y Anthrosoles (de acuerdo a WRB, FAO, 1998) característicos del paisaje de morrenas del Norte de Alemania. La Catena fue cultivada con trigo (Tritricum aestivum) bajo un sistema de manejo convencional. La pendiente de la Catena es de 7°.
Recolección de las muestras
Se recolectaron muestras no disturbadas de suelo en los distintos horizontes de los sitios CIIS1, CIIS2 y CIIS3 de una catena de suelos (Catena II, sitios 1, 2 y 3 respectivamente, Cuadro 1). Las muestras fueron tomadas en cilindros metálicos de 100cm3 con un equipo neumático en ángulos de 0º (vertical) y 90º (horizontal) con respecto a la superficie del suelo. El equipo neumático permitió caracterizar la anisotropía de las propiedades hidráulicas sin alterar la estructura del suelo durante el muestreo. Con las muestras no disturbadas de suelo se determinó la curva de retención de agua (4 repeticiones) y la conductividad hidráulica en fase saturada (kf, 10 repeticiones).
 |
PT: Porosidad
Total; PDR: Poros de Drenaje Rápido; PDL: Poros de Drenaje Lento; PAU:
Poros de Agua Útil; PAI: Poros de Agua Inútil. PA: Pie de arado; sub: bloque subangular; lam: laminar, ang: bloque angular |
Determinación de la curva de retención de agua
Las muestras de suelo fueron saturadas con agua por medio de ascenso capilar. La saturación tomó al menos dos días, con el objetivo de evitar inclusiones de aire en los poros del suelo. Posteriormente, las muestras fueron equilibradas a los siguientes potenciales mátricos: -10, -20, -30 hPa en bandejas de arena, -60, -150, -300; -500 hPa en platos cerámicos (método succión) y -15000 hPa en ollas de presión. Una vez que las muestras alcanzaron un equilibrio con el potencial mátrico aplicado, se determinó el contenido de agua. Para determinar la densidad aparente, las muestras se secaron en una estufa a 105ºC por 16 horas. Para el cálculo de la porosidad total (PT) se usó un valor de densidad real de 2,65 g cm-3.
Determinación de la conductividad hidráulica saturada
La determinación de la conductividad hidráulica saturada (kf) se realizó mediante un permeameómetro de Haube bajo condiciones no estacionarias, tal como lo describen Hartge y Horn (1989). Cada medición se repitió 3 veces.
Modelación del transporte de agua en la Catena
Con el objetivo de dimensionar el efecto de las propiedades hidráulicas sobre el movimiento de agua en fase saturada, se modeló el transporte 2D a lo largo de la Catena con el software Hydrus 2D (Simunek et al., 2003).
Para la modelación se definieron las propiedades hidráulicas del suelo, el monto diario de las precipitaciones y evapotranspiración y las condiciones de borde e iniciales del suelo. A partir de la curva de retención de agua y kf se estimó la conductividad hidráulica no saturada de cada horizonte de suelo de acuerdo con el modelo de van Genuchten (1980). Anisotropía de kf se consideró para los 2 primeros horizontes de suelo. La evapotranspiración del trigo se calculó a partir del método propuesto por Allen (DVWK, 1996). En la Figura 1 se presentan los horizontes de suelo y las condiciones de borde consideradas en el modelo. La modelación se realizó desde octubre del 2002 a diciembre del 2003. Inicialmente el suelo se encontraba completamente saturado con agua.
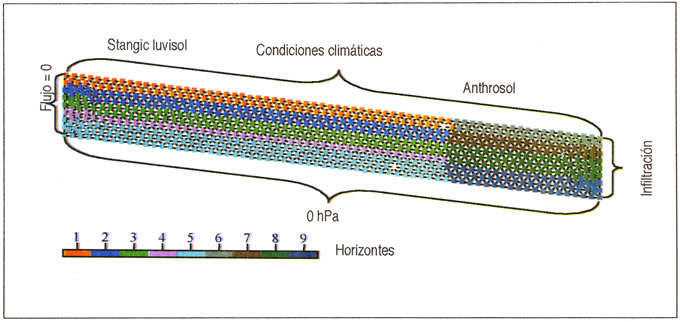 |
| Figura 1: Condiciones
de borde de la simulación del transporte de agua Figure 1: Boundary conditions of the water transport simulation |
Análisis estadístico
Debido a que los valores de kf no presentan una distribución normal, estos fueron transformados a logaritmos tal como lo sugieren Hartge y Horn (1989). Se determinaron los promedios para cada horizonte de suelo y dirección de muestreo. Con el propósito de determinar el efecto de la dirección del muestreo sobre las propiedades analizadas, se realizó un análisis de varianza (p ≤ 0,05). Las diferencias entre las medias se determinaron mediante un Test de Tukey (p ≤ 0,05).
RESULTADOS
Características generales de la catena
Los distintos tipos de suelo, especialmente el Stagnic Luvisol en CIIS1 y CIIS2, y en menor medida el Anthrosol en CIIS3 presentan una clara diferenciación de horizontes. En CIIS1 y CIIS2 son destacables las diferencias texturales entre horizontes, las que sumadas al efecto del manejo del suelo en los primeros 30cm y a las condiciones climáticas, determinan la estructura y la magnitud y distribución del sistema poroso (Cuadro 1). El alto porcentaje de arena es un común denominador de todos los horizontes de suelo con excepción del horizonte Btg en CIIS1.
La estructura subangular y laminar presentes en la cama de semillas (horizonte Ap) y en el pie de arado (P.A.) son consecuencia de las labores de suelo. La estructura laminar, típica de un pie de arado, se manifiesta en la reducción del volumen poroso y en la redistribución de los poros del suelo, especialmente en CIIS1 y CIIS2. La estructura laminar se caracteriza por presentar un eje horizontal mayor al vertical mientras que la subangular presenta ejes equidistantes.
La porosidad refleja la textura y estructura del suelo. Los horizontes (Ap y Bv) que presentan un mayor contenido de arena se caracterizan por tener un mayor volumen de PDR y menor volumen de PAI en contraste con el horizonte de acumulación de arcilla (Btg), en donde el volumen de PDR puede llegar sólo a un 1,4% y los PAI superan el 17%.
Conductividad hidráulica saturada
La Figura 2 presenta los valores para kf de cada uno de los horizontes de suelo de la catena. En general se puede observar que kf es heterogénea en CIIS1 y CIIS2, lo que es consecuencia de las distintas características que presenta el medio poroso en cada uno de sus horizontes. La homogeneidad textural y estructural observada en los horizontes del Anthrosol (CIIS3) es también registrada en kf.
La conductividad hidráulica en fase saturada presenta un comportamiento anisotrópico significativo en varios horizontes de suelo, lo que está estrechamente ligado con la estructura del suelo. En horizontes con estructura laminar se observa que kf-H > kf-V y en aquellos con estructura subangular generalmente se observa isotropía en kf salvo algunas excepciones en donde kf-V > kf-H.
Modelación movimiento de agua
Para demostrar el efecto que tiene la anisotropía de kf sobre el movimiento de agua en fase saturada, se modeló el transporte de agua para dos escenarios A) kf-V = kf-H y B) kf-V < kf-H. Para ello se consideraron los valores de kf vertical y horizontal de la cama de semillas y del pie de arado.
Se seleccionó el día 325 de la modelación (Figura 3) ya que en dicho día se alcanzó un alto grado de saturación de agua en todo el perfil de suelo, lo que esta representado por los bajos valores tensión de agua (cercanos a 0 hPa).
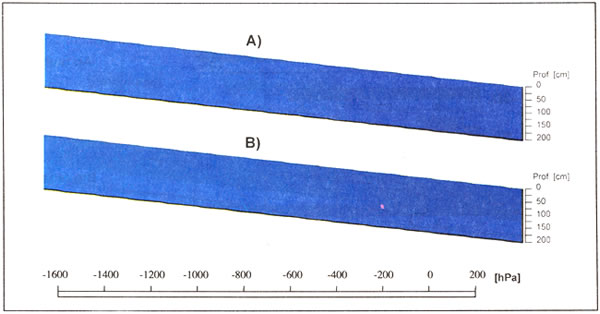 |
Figura
3: Potencial mátrico en el perfil de suelo de la catena con A) kf-V
= kf-H y B) kf-V < kf-H Figure 3: Matrix potential of the soil profile of the catena with A) kf-V = kf-H y B) kf-V < kf-H |
La Figura 4 presenta los vectores del flujo de agua para los escenarios A y B. Cuando la conductividad hidráulica es isotrópica, o sea kf-V = kf-H, el movimiento de agua bajo condiciones de saturación se rige fundamentalmente por la gradiente hidráulica generada por el evento de lluvia, o sea, los vectores del flujo de agua se dirigen hacia la napa freática (tensión de agua 0 hPa). Sin embargo, cuando se considera la anisotropía de kf, el flujo de agua es desviado en dirección del máximo componente de kf (kf-H > kf-V), lo que implica un desvío del flujo en dirección de la pendiente, produciéndose con ello, un flujo lateral de agua.
DISCUSION
El efecto de la textura y del manejo sobre las propiedades estructurales del suelo se encuentran ampliamente documentadas en la literatura (Ehlers, 1973; Ball, 1981; Ellies et al., 1996; Ahuja et al., 1998; Hartge y Horn, 1999). Sin embargo, no son tanto los trabajos que han relacionado la estructura de un suelo con el comportamiento (an)isotrópico de la conductividad hidráulica saturada (por ejemplo Dörner y Horn, 2006) y muchos menos los que analizan su efecto sobre el movimiento de agua en una pendiente (Tigges, 2000; Ursino et al., 2001).
La conductividad hidráulica está fuertemente ligada a la estructura del suelo, al volumen de poros estructurales (o porosidad efectiva según Ahuja, et al., 1984) y a la continuidad e interconexión del medio poroso. Es por ello que la forma y dimensión de los agregados que forman el suelo cumplen un rol fundamental en la generación de vías de paso para el movimiento del agua en fase saturada. La compactación en un pie de arado permite la formación de agregados laminares cuya sección horizontal es mayor a la vertical, lo que trae consecuencias no tan sólo en una reducción de la conductividad hidráulica vertical, sino que también permite un aumento de la componente horizontal de kf debido a la mayor continuidad entre los agregados laminares. Dicho efecto estructural disminuye con el secado del suelo tal como lo demostraron Tigges (2000), Ursino et al. (2001) y Dörner y Horn (2005).
Si bien es cierto que se puede modelar el efecto de la formación de un pie de arado sobre el transporte de agua en fase saturada en una pendiente, dicho efecto debe ser validado con registros de potencial mátrico y/o contenido volumétrico de agua in situ, ya que las propiedades que dependen de la estructura presentan una gran variabilidad espacial (Nielsen y Wendroth, 2003). Sin perjuicio de lo anterior y asumiendo que la estrata compactada es continua resulta evidente que se debe considerar el efecto que tiene la formación de un pie de arado en la generación de flujos laterales de agua sumado a los ya ampliamente conocidos, como aumento en la resistencia a la penetración y densidad aparente, disminución de la porosidad estructural e incremento en la difusión térmica.
CONCLUSIONES
La anisotropía de la conductividad hidráulica saturada está estrechamente ligada a la estructura que presenta el suelo.
La formación de un pie de arado puede generar movimiento lateral de agua en una pendiente.
AGRADECIMIENTOS
El primer autor agradece al DAAD (Servicio Alemán de Intercambio Académico) por el financiamiento de una beca de doctorado en la Universidad Christian Albrechts de Kiel.
BIBLIOGRAFIA
AHUJA, L.R.; NANEY, J.W.; GREEN, R.E.; NIELSEN, D.R. 1984. Macroporosity to characterize spatial variability of hydraulic conductivity and effects of land management. Soil Sci. Soc. Am. J. 48: 699-702.
AHUJA, L.R.; FIEDLER, F.; DUNN, G.H.; BENJAMIN, J.G.; GARRISON. 1998. Changes in Soil Water Retention Curve due to Tillage and Natural Reconsolidation. SSSAJ 62: 1228-1233.
BALL, B.C. 1981: Pore characteristics of soils from two cultivation experiments as shown by gas diffusivities and permeabilities and air-filled porosities. J. of Soil Sci. 32: 483-498.
BEAR, J.; BREASTER, C.; MENIER, P.C. 1987. Effective and Relative Permeabilities of Anisotropic Porous Media. Transport in Porous Media, 2: 301-316.
DABNEY, S.M.; SELIM, H.M. 1987. Anisotropy of a fragipan soil: vertical vs. horizontal hydraulic conductivity. Soil Sci. Soc. Am. J. 51: 3-6.
DEUTSCHER VERBAND FÜR WASSERWIRTSCHAFT UND KULTURBAU e. V. (DVWK) (1996): Ermittlung der Verdunstung von Land- und Wasserflächen. Bearbeitet vom DVWK – Fachausschuss "Verdunstung". Bonn. 135 p.
DÖRNER, J.; HORN, R. 2005. Anisotropie von Porenfunktionen und ihre Auswirkung auf die Wasserbewegung in einer Jungmoränenlandschaft Schleswig-Holstein. Mit. der DGB 106: 9-10.
DÖRNER, J.; HORN, R. 2006. Anisotropy of pore functions in structured Stagnic Luvisols in the Weichselien moraine region in N Germany. J. Plant. Nutr. Soil Sci. 169: 213-220.
DÖRNER, J.; DEC, D. 2007. La permeabilidad del aire y conductividad hidráulica saturada como herramienta para la caracterización funcional de los poros del suelo. Rev. Ciencias Suelo Nutr. Veg. 7 (2): 1-13.
EHLERS, W. 1973. Gesamtporenvolumen und Porengrößenverteilung in unbearbeiteten und bearbeiteten Lößböden. Zeitschrift für Pflazenernährung und Bodenkunde 134: 193-206.
ELLIES, A.; SMITH, R.; HORN, R. 1996. Transmisión de tensiones en el perfil de algunos suelos. Agro Sur 24: 149-158.
ELLIES, A; GREZ, R.; RAMIREZ, C. 1997. La conductividad hidráulica en fase saturada como herramienta para el diagnóstico de la estructura del suelo. Agro Sur 25: 51-56.
FAO. 1998. World Reference Base for Soil Resources. World Soil Resources Report 84, Food and Agriculture Organisation of the United Nations, Rome.
FAZEKAS, O. 2005. Bedeutung von Bodenstruktur und Wasserspannung als stabilisierenre Kenngrö≤en gegen intesive mechanische Belastungen in einer Parabraunerde aus Löss unter Pflug- und Mulchsaat. Tesis Doctorado en Ciencias Agrarias, Universidad Christian Albrechts de Kiel, Nr. 67, 170 p. ISBN: 0933-680X.
HARTGE, K.H. 1984. Vergleich der Verteilungen der Wasserleitfähigkeit und des Porenvolumens von waagerecht and senkrecht entnommenen Stechzylinderproben. Zeitschrift für Pflanzenernähr. und Bodenkunde 147: 316–323.
HARTGE, K.H.; HORN, R. 1989. Die physikalische Untersuchung von Böden. Stuttgart, Enke, 177 p.
HARTGE, K.H.; HORN, R. 1999. Einführung in die Bodenphysik. Enke, Stuttgart, 304 p.
HORN, R.; SMUCKER, A. 2005. Structure formation and its consequences for gas and water transport in unsaturated arable and forest soils. Soil and Tillage Research 82: 5-14.
MUALEM, Y. 1984. Anisotropy of unsaturated soils. SSSAJ 48: 505-509.
NIELSEN, D.R.; WENDROTH, O. 2003. Spatial and Temporal Statistics: sampling soil fields and their vegetation. GeoEcology, Catena Verlag GMBH, Reiskirchen, 398 p.
SIMUNEK, J., SENJA, M. und VAN GENUCHTEN, M. Th. 2003. The Hydrus 2D Software Package for Simulating the Two – Dimensional Movement of Water, Heat, and Multiple Solutes in Variably – Saturated Media. Version 2.102. U.S. Salinity Laboratory, U.S. Department of Agriculture, Agricultural Research Service, Riverside, California. 227 p.
TIGGES, U. 2000. Untersuchungen zum mehrdimensionalen Wassertransport unter besonderer Berücksichtigung der Anisotropie der hydraulischen Leitfähigkeit. Dissertation, Kiel. 145 p.
URSINO, N.; GIMMI, Th.; FLÜHLER, H. 2001. Combined Effects of Heterogeneity, Anisotropy, and Saturation on Steady State Flow and Transport: A Laboratory Sand Tank Experiment. Water Resources Research 37: 201-208.
VAN GENUCHTEN M. Th. (1980): A closed – form equation for predicting the hydraulic conductivity of unsaturated soils. SSSAJ 44: 892–898.
YOUNGS, E.C. 1991. Hydraulic conductivity of saturated soils, in: K.A. Smith and C.E. Mullins (eds.): Soil Analysis – Physical Methods. Marcel Dekker, New York, p. 161-207.
ZASLAVSKY, D.; ROGOWSKI, A.S. 1969. Hydrologic and morphologic implications of anisotropy and infiltration in soil profile development. Soil Sci. Soc. Am. Proc. 33: 594-599.
Recepción de originales: 20 de enero de 2008