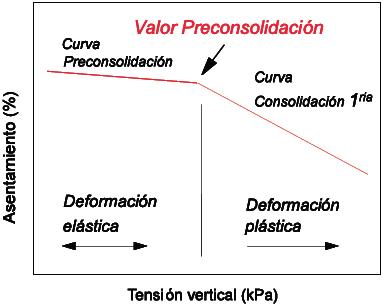
Figure 1: Schematic representation of the soil bearing capacity. Adapted from Horn (1981).
Agro Sur 37(3) 220-231 2009
DOI:10.4206/agrosur.2009.v37n3-06
ARTÍCULOS ORIGINALES
DETERMINACIÓN DE LA CAPACIDAD DE SOPORTE DE UN ANDISOL (DURIC HAPLUDAND) POR MEDIO DE DOS MÉTODOS GRÁFICOS 1
DETERMINATION OF PRECOMPRESSION STRESS OF AN ANDISOL (DURIC HAPLUDAND) USING TWO GRAPHIC METHODS
Marcelo Payahuala y José Dörner
Instituto de Ingeniería Agraria y Suelos, Facultad Ciencias Agrarias, Universidad Austral de Chile. josedorner@uach.cl.
ABSTRACT
The graphical method of Casagrande (1936) has been widely used in southern Chile to determine the soil bearing capacity, but no evaluation has been conducted to determine whether this method is better than that proposed by Pacheco Silva (1970) which is characterized by its simplicity, objectivity and more appropriability for use in soils with a high deformation capacity such as Andisols. Therefore, both of these graphical methods to determine the bearing capacity were compared using soil samples collected in an Andisol under 4 different types of pasture and applying successive loads to the soil samples during the consolidation experiment. To compare both methods, different graphical scales and the objectivity defined by the determination of the bearing capacity by different users were considered. Additionally, the relationship between this soil property and the penetration resistance measured on the field was determined. The results from both methods were well related when they were compared using a 1:1 graphic scale. The Pacheco Silva method presented lower values than Casagrande method. The latter is more subjective due to the interpretation by the user compared with the Pacheco Silva method; however, mathematically it has a better interpretation of the infection point between the elastic and plastic deformation. Finally, the precompression stress defined by both methods increased with an increase in the penetration resistance of the soil measured in the field.
Key words: Bearing capacity, Andisol, Casagrande and Pacheco-Silva methods, precompression stress.
RESUMEN
En el sur de Chile se ha utilizado ampliamente el método gráfico de Casagrande (1936) para determinar la capacidad de soporte del suelo, sin evaluar si el método es mejor que otros como el propuesto por Pacheco Silva (1970) que se caracteriza por ser de fácil determinación, objetivo y más apropiado para suelos con alta capacidad de deformación, como los Andisoles. Para resolver esa pregunta, se compararon dos métodos de determinación gráfica de la capacidad de soporte, el método descrito por Casagrande (1936) y el de Pacheco Silva (1970), utilizando muestras de un Andisol bajo 4 tipos de pradera y aplicando sucesivas cargas sobre muestras de suelo en un ensayo de consolidación. En la comparación de los métodos, se consideró el efecto de distintas escalas gráficas y la objetividad por medio de la determinación de la capacidad de soporte por varios usuarios. Adicionalmente, se determinó la relación de esta propiedad del suelo con la resistencia a la penetración determinada en terreno.
Los métodos analizados se relacionan de muy buena forma cuando son comparados en una escala gráfica 1:1, presentando el método de Pacheco Silva valores levemente inferiores que el de Casagrande. Este último resultó ser más subjetivo frente a la interpretación del usuario que el de Pacheco Silva; sin embargo, matemáticamente da una mejor interpretación del punto de inflexión entre la deformación elástica y plástica. Finalmente, se determinó que la capacidad de soporte determinada por ambos métodos aumenta con el incremento de la resistencia a la penetración medida en terreno.
Palabras claves: Capacidad de soporte, Andisol, métodos de Casagrande y Pacheco Silva, valor de precomprensión.
INTRODUCCIÓN
La estructura del suelo juega un rol muy importante en el almacenamiento y transporte de agua y aire (Dörner y Horn, 2006), el transporte de calor (Dec et al., 2009), el desarrollo radical (Ellies, 1988; Ellies y Contreras, 1997) y en la estabilidad mecánica del suelo (Horn et al., 2002), entre otras. Una mala estructura, por ejemplo, puede significar efectos dañinos para el cultivo (Taboada, 2007) o incrementar los riesgos de escurrimiento superficial y subsuperficial (Dörner y Dec, 2008); por el contrario, una buena estructura hace que los factores del crecimiento funcionen a su máxima eficiencia y se obtengan mayores rendimientos en las cosechas (Gavande, 1972), como también que el agua infiltre en el perfil sin que ocurra escurrimiento superficial ni arrastre de sedimentos y nutrientes (Alfaro y Salazar, 2008; Dörner y Dec, 2008). La estructura de un suelo puede cambiar como consecuencia de fuerzas externas (e.g. compactación en Ellies, 1988, Horn et al., 2002, entre otros), internas (ciclos naturales de humectación y secado en Dörner et al., 2009) y por la actividad biológica (e.g. Angulo-Jaramillo et al., 1997). Los principales cambios en la estructura que tienen un efecto negativo sobre la producción agrícola y medio ambiente, ocurren cuando el suelo es sometido a presiones que no es capaz de sostener (Horn et al., 1995). Lo anterior, se puede evitar si conocemos previamente la estabilidad mecánica del suelo: su resistencia al corte y la capacidad de soporte. Mientras la primera nos permite conocer la cohesión interna de los agregados de suelo, la segunda corresponde a la máxima carga que puede soportar un suelo sin que presente una deformación de carácter plástico con pérdida de porosidad (Terzaghi y Peck, 1963; Horn, 1981). Esta última propiedad es usada ampliamente en mecánica de suelos para evaluar su estabilidad, ya que permite determinar la tensión máxima a la que ha sido sometida el suelo.
La capacidad de soporte de un suelo depende de su textura, estructura, contenido de agua, la presencia de materia orgánica y el historial de manejo (Horn, 1981; Ellies, 1988). Según Berry y Reid (1993), cuando un suelo es sometido a una gran carga, se produce en un exceso de presión de agua intersticial; debido a que ésta no puede resistir esfuerzos cortantes, el exceso de presión intersticial se disipa mediante un flujo de agua hacia el exterior. La disipación de este exceso de presión debida al flujo de agua hacia el exterior se denomina consolidación, proceso que tiene dos consecuencias importantes: i) conduce a una reducción del volumen de poros y, por lo tanto, a una reducción del volumen total de la masa de suelo, lo cual se manifiesta en el asentamiento de la superficie del terreno y, por consiguiente, en un reordenamiento de la estructura; ii) durante la disipación del exceso de presión intersticial, el esfuerzo efectivo en la masa de suelo aumenta y, por tanto, se incrementa su resistencia al corte. La consolidación y la resistencia al corte son, por lo tanto, procesos que se relacionan mutuamente.
La capacidad de soporte se determina con un ensayo que se conoce como ensayo de consolidación, mediante la utilización de un odómetro y por medio de la aplicación de presiones sucesivas sobre el suelo. Con ello, el suelo se compacta y esa deformación es registrada con un micrómetro. Según Horn (1981), la determinación de la capacidad de soporte o valor de preconsolidación pasa por definir aquel punto a partir del cual la deformación del suelo pasa de ser reversible (elástica) a irreversible (plástica, Figura 1). Para la determinación gráfica de la capacidad de soporte existen varios métodos, dentro de los cuales destacan el método de Casagrande (1936) y el método de Pacheco Silva (1970). La utilización de estos métodos gráficos puede ser compleja. Clementino (2005) menciona que el método de Pacheco Silva es de fácil y rápida determinación. Por otro lado, indica que a diferencia del método de Casagrande, no requiere de una interpretación que muchas veces es subjetiva y que los resultados que se obtienen son independientes de la escala a la cual están siendo evaluados. Por lo tanto, concluye que este método es ideal para analizar suelos blandos, donde pequeños cambios de compresibilidad en el suelo no son magnificados. En suelos volcánicos del sur de Chile se ha usado ampliamente el método de Casagrande (e.g. Ellies, 1988; Seguel, 2006; Dörner et al., 2009) sin evaluar si es el mejor método para determinar la capacidad de soporte o si sus resultados difieren del método de Pacheco Silva, que es recomendado para suelos de baja densidad como los Andisoles. Es por ello que los objetivos de este trabajo son: i) determinar la capacidad de soporte del suelo evaluada por dos métodos (Casagrande y Pacheco Silva) en distintos tipos de praderas, ii) comparar ambas metodologías de determinación de la capacidad de soporte del suelo usando distintas escalas gráficas, iii) determinar la subjetividad de ambas metodologías al ser utilizadas por distintos usuarios y iv) relacionar la capacidad de soporte con la resistencia a la penetración del suelo.
MATERIAL Y METODO
Suelos y manejo
Un Andisol de la Serie Valdivia (Duric Hapludand, CIREN, 2003) fue utilizado para comparar dos métodos para la determinación de la capacidad de soporte. El suelo es moderadamente profundo, ocupa una posición de terrazas remanentes en la depresión de San José, a una altura de 9 a 20 m.s.n.m. Superficialmente, presenta una textura franco limosa que se vuelve más gruesa en profundidad. El substrato corresponde a una toba, deposito de materiales volcánicos de fuerte compactación y mezclado con clastos alterados, el cual se denomina localmente cancagua. La topografía es compleja, suavemente ondulada con 5 a 8% de pendiente y con buen drenaje. El clima corresponde a uno templado lluvioso, con una temperatura promedio de 12,2 °C y con una amplitud térmica reducida debido a la cercanía que tiene al mar y a los lagos. Las precipitaciones se presentan durante todo el año, pero tiene una estación más marcada que es el invierno. El promedio de precipitaciones se ubica entre los 2272 mm aproximadamente.
El suelo es usado para sostener 4 tipos de praderas considerando tres estrategias para el mejoramiento de una que se encuentra degradada. Los tratamientos son: T1: pradera degradada (control); T2: pradera degradada + fertilizantes; T3: pradera sembrada con Lolium perenne y Trifolium repens + fertilizantes; y T4: pradera sembrada polifítica de L. perenne, T. repens, Dactilis glomerata, Bromus valdivianus y Holcus lanatus + fertilizante. Las praderas se establecieron en septiembre de 2006.
Análisis de terreno y recolección de muestras de suelo
En junio de 2007 se determinó la resistencia a la penetración in situ. Para esto se utilizó un penetrómetro de punta cónica (Wykeham Farrance) y se procedió a muestrear en terreno con una separación de 2,5 metros siguiendo un diseño cuadricular (n: 147 por tratamiento). Los registros fueron ordenados y se transformaron en una misma unidad de medida de presión (kPa).
Junto con el análisis in situ, se definieron tres parcelas por tratamiento de 20 x 20 m2, en las cuales se recolectaron muestras no disturbadas de suelo contenidas en cilindros metálicos de 110 cm3 (altura: 3 cm; diámetro: 6,89 cm). Los cilindros se extrajeron a 5 cm de profundidad en puntos cercanos a los utilizados para definir la resistencia a la penetración. Se recolectaron cuatro repeticiones por parcela, completando 12 muestras por tratamiento y 48 en total.
Ensayo de consolidación
Antes de la realización del ensayo de consolidación, las muestras fueron saturadas por ascenso capilar de agua y luego equilibradas a -60 hPa de presión (correspondiente a la capacidad de aire del suelo) mediante la utilización de bandejas de arena con control del nivel freático. Cuando las muestras alcanzaron un equilibrio hidrostático, fueron retiradas de la bandeja, pesadas y colocadas en un odómetro (Controls, T 303) para determinar la curva de consolidación, la que fue realizada con muestras confinadas con drenaje libre (Kézdi, 1980). Para ello, las muestras de suelo se colocaron en un anillo de bronce con sus respectivas placas porosas. El anillo de bronce se instaló en la cajuela del odómetro. Posteriormente, se colocó la placa porosa sobre la muestra, ajustando el micrómetro y agregando cargas de 6,25 – 12,5 – 25 – 50 – 100 – 200 y 400 kPa durante 6 minutos cada una. Finalmente, se procedió a retirar los pesos de la siguiente manera: se retiraron 400 kPa, seis minutos después se retiraran 200 kPa y así sucesivamente, retirando 100; 87,5; 6,25 kPa, leyendo el micrómetro al final del lapso de cada peso.
Determinación de la capacidad de soporte del suelo
La determinación de la capacidad de soporte se realizó según el método gráfico descrito por Casagrande (1936) y por el método propuesto por Pacheco Silva (1970). La Figura 2 muestra una curva resultante de un ensayo de consolidación y la definición de la capacidad de soporte por medio de ambos métodos gráficos.
El método de Pacheco Silva (1970) se determina de la siguiente manera:
i) Se traza una recta horizontal C-D paralela al eje X (presión) y que pasa
por el punto C (0,e0).
ii) Se construye
la recta A-B correspondiente a la extensión de la línea de consolidación primaria,
cuya prolongación intercepta a la recta C-D.
iii) Desde el punto de intercepción de ambas rectas, se traza una recta perpendicular
al eje X (presión), la cual intercepta a la curva en un punto E.
iv) Por el
punto E se traza otra recta paralela al eje X (presión), la cual intercepta
a la recta A-B en el punto F.
v) Por el
punto F, se traza una recta perpendicular al eje X (presión), la cual intercepta
a dicho eje en el punto de abscisa C.S., obteniendo así el valor de preconsolidación
o capacidad de soporte.
Para definir la capacidad de soporte de acuerdo al método gráfico de Casagrande (1936):
i)
Se traza la recta A-B correspondiente a la prolongación
de la línea de consolidación primaria.
ii) Se ubica
el punto de la curva que presenta el radio
de curvatura máxima (punto de inflexión) el
cual corresponde al punto C. Se construye una
tangente D-E que pasa por dicho punto C.
iii) Se traza
una recta C-F paralela al eje X (presión).
iv) Se construye
una bisectriz C-G del ángulo FCE
v) Desde
la intersección entre las rectas C-G y A-B
(punto H) se traza una recta perpendicular al
eje X (presión), hasta interceptarse con dicho eje
en el punto de abscisa C.S., obteniéndose así
el valor de preconsolidación o capacidad de soporte.
Para determinar el efecto de la escala gráfica sobre la determinación de la capacidad de soporte, se compararon ambos métodos con una relación gráfica de ancho y alto de 1:1, 2:1 y 1:2. La magnitud de los ejes x (1 a 1000 kPa) e y (0 a 10mm con una deformación que fluctuó entre 5 y 9mm entre todas las muestras) fue la misma en todos los casos, Finalmente, con el fin de analizar la objetividad del método entre diferentes usuarios se eligieron tres muestras al azar las cuales fueron determinadas por diferentes personas.
Diseño experimental y análisis estadístico
El diseño experimental aplicado fue de cuatro tratamientos con tres repeticiones distribuidas completamente al azar. Cada parcela (repetición) fue de 20x20 m (400 m2), así la superficie experimental total fue de 4.800 m2.
Para el análisis estadístico se utilizó el programa computacional Statgraphics Plus 5.1; en un diseño de distribución completamente al azar. Se realizó un análisis de varianza (ANDEVA) para determinar diferencia estadística con un nivel de significancia de 95%.
RESULTADOS Y DISCUSIÓN
Efecto de los tratamientos sobre la capacidad de soporte.
La Figura 3 presenta la capacidad de soporte determinada por los métodos de Casagrande y Pacheco Silva para cuatro tipos de praderas. Se puede apreciar que existen diferencias estadísticamente significativas entre todos los tratamientos (p ≤ 0,05). Las praderas que no presentaron labores de intervención mecánica (T1 y T2) presentaron los valores más altos de capacidad de soporte. Según Ellies y Contreras (1997), la capacidad de soporte está muy ligada a la densidad aparente y con ello al manejo del suelo, por lo que esta disminuye en los sitios donde el suelo se laborea frecuentemente, ya que al soltar el suelo, baja la densidad aparente y con ello la capacidad de soporte. Los suelos que no han sido labrados presentan una mayor estructuración, llegándose a establecer una secuencia de resistencia desde los materiales masivos hasta la estructura de bloques subangulares, la que presentaría una mayor resistencia a la deformación debido a la mayor cantidad de puntos de contacto entre los agregados (Seguel, 2006). Los valores de capacidad de soporte observados (Figura 3), coinciden con los presentados por Seguel y Orellana (2008), quienes muestran valores para diferentes Andisoles, calculados con el método de Casagrande (1936), con intervalos de carga de 10 minutos y un potencial mátrico de 60 kPa, presentando valores desde los 60 kPa hasta un poco más de los 80 kPa para la Serie Osorno (Typic Hapludand).
Junto con el efecto de los tratamientos, se puede observar que existen diferencias estadísticamente significativas (p ≤ 0,05) en la determinación de la capacidad de soporte según el método empleado, en donde los mayores valores fueron determinados con el método de Casagrande. Esta situación concuerda con lo encontrado por Ortigao (1995), quien determinó en un ensayo de consolidación que el valor de capacidad de soporte varía entre 34 y 30 kPa para los métodos de Casagrande y Pacheco Silva, respectivamente. En ese mismo sentido, la Figura 4 muestra un R2 de 0,94 ubicándose la relación entre ambos métodos muy cercana a la línea 1:1, siendo los valores determinados a partir del método de Casagrande generalmente mayores. A conclusiones similares llegaron Grozic et al. (2005). Por otro lado, Dias Junior y Pierce (1995) al probar una combinación de metodologías graficas para determinar la presión de consolidación determinó que el mejor procedimiento fue aquel que obtuvo un R2 de 0,92 y cuyos puntos se encontraban muy cerca de la línea 1:1, tal como en el presente trabajo.
Como se presenta en la Figura 2, el método de Casagrande arroja un valor ligeramente superior al de Pacheco Silva, lo que está dado por la intercepción que presenta la bisectriz (C-G Figura 2 Casagrande) con la recta A-B (de la misma Figura) con respecto a la intercepción de la perpendicular al eje Y (E-F Figura 2 Pacheco Silva)2 con la recta A-B (misma Figura), ya que el punto de inflexión C (Figura 2 Casagrande) es muy similar al punto E (Figura 2 Pacheco Silva). La diagonal (D-E Figura 2 Casagrande) como recta tangente al gráfico es una mejor aproximación local que la recta perpendicular (E-F Figura 2 Pacheco Silva), ya que se aproxima más al valor de la derivada de la curva en el punto, por lo que la tangente es la mejor aproximación lineal (local) al gráfico de la curva en el punto de preconsolidación y mientras más se aproxime la bisectriz a la tangente, más precisa es la aproximación. A partir de esto, se puede afirmar que el método de Casagrande es más preciso en comparación con el método de Pacheco Silva, ya que es el que más se aproxima al punto de preconsolidación debido a que la bisectriz (C-G Figura 2 Casagrande) siempre se encontrará más próxima a la recta tangente (D-E misma Figura) que la diagonal (E-F Figura 2 Pacheco Silva) . Una forma práctica de probar cual método es más asertivo en determinar el punto de preconsolidación, sería determinar la capacidad de soporte de varias muestras de un mismo suelo (e.g. material tamizado a 2 mm en muestras ensambladas a una misma densidad aparente) por medio de ambos métodos gráficos. Posteriormente, cuando se haya determinado el punto de preconsolidación por ambos métodos, aplicar presiones equivalentes a los valores determinados a muestras del mismo suelo, con el fin de determinar posteriormente su resiliencia volumétrica, para así saber cual método se aproxima más a la definición de capacidad de soporte: “presión máxima que es capaz de soportar el suelo sin que se reduzca irreversiblemente su volumen poroso” (Horn, 1981).
Efecto de la escala gráfica sobre la determinación de la capacidad de soporte a través de dos métodos.
Las Figuras 5 y 6 presentan el efecto de la escala gráfica (2:1 y 1:2) sobre la determinación de la capacidad de soporte según los métodos de Casagrande y Pacheco Silva.
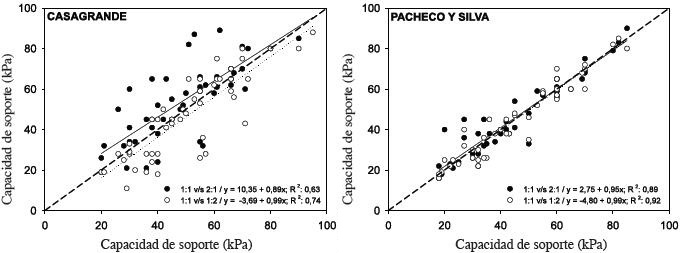 |
Figura
6: Relación entre las escalas gráficas para la determinación de la capacidad
de soporte del
suelo. Figure 6: Relationship between the graphic scales to determine the soil bearing capacity. |
Con el método de Casagrande se observan diferencias estadísticamente significativas (p ≤ 0,05) al determinar la capacidad de soporte con distintas escalas gráficas (Figura 5). Lo anterior no se observó al utilizar el método de Pacheco Silva (P ≤ 0,05). Al relacionar los resultados de las escalas 2:1 y 1:2 con los de la escala 1:1 (Figura 6) se puede apreciar que existen diferencias entre los métodos utilizados. Con el método de Casagrande, las escalas 2:1 (y = 10.35 + 0,89x; R2: 0,89) y 1:2 (y = -3.69 + 0,99x; R2: 0,74) tienden a sobre y subestimar los valores de capacidad de soporte al compararlos con la línea 1:1, respectivamente. Por el contrario, los resultados evaluados con el método de Pacheco Silva presentan pendientes mayores a 0,95 y R2 sobre 0,89 concentrándose en la línea 1:1 sin presentar mayores diferencias en función de la escala gráfica. Estos resultados concuerdan con lo que afirma Clementino (2005), al mencionar que la determinación de la capacidad de soporte por medio del método de Casagrande depende de la escala gráfica a la cual están siendo evaluadas, mientras que el de Pacheco Silva no se ve afectado por dicha situación. Las modificaciones que se aprecian en el caso del método de Casagrande se deben a que al cambiar la escala gráfica se modifica la curva, teniendo efectos sobre la bisectriz (el ángulo de la bisectriz es dependiente de la curvatura de la curva4). En el caso del método de Pacheco Silva la perpendicularidad de la recta (E-F en Figura 2 P.S.) no varía con la curvatura de la curva, es por eso que el punto de preconsolidación no se ve afectado.
Objetividad de los métodos frente a diferentes usuarios.
Con el fin de determinar la objetividad que tienen ambos métodos gráficos para la determinación de la capacidad de soporte, se escogieron tres muestras completamente al azar, de tratamientos y escalas gráficas diferentes. Cada una de estas curvas fue utilizada para la determinación de la capacidad de soporte siguiendo ambos métodos, esta vez por tres diferentes usuarios. Estos usuarios desconocían con anterioridad la metodología de determinación de la capacidad de soporte a través de estos métodos gráficos y fueron entrenados con este objeto.
En el Cuadro 1 se puede apreciar que las muestras determinadas por el método de Pacheco Silva presentaron en general diferencias estadísticamente significativas en sus promedios con el método de Casagrande (p ≤ 0,05). También existió una mayor objetividad (Pacheco Silva) al ser sometidos a diferentes usuarios, ya que presentó un error medio aproximado de sólo un 2%. Además, se puede apreciar que los resultados con el método de Pacheco Silva resultaron ser más homogéneos (promedio del coeficiente de variación Pacheco Silva: 8 %; Casagrande: 21%) lo que se debe a que en el método de Casagrande (Figura 2), la determinación del punto de inflexión (punto C) resulta más difícil de obtener, por lo que puede variar entre diferentes usuarios. Clementino (2005) y Ortigao (1995) afirman que el método de Pacheco Silva, a diferencia del método de Casagrande, es más independiente y objetivo frente a diferentes operadores. Para evitar la subjetividad del método de Casagrande es necesario determinar la ecuación de la curva y de esta manera determinar el punto de máxima curvatura (punto C), para así eliminar el factor “usuario”, obteniendo un método objetivo y que matemáticamente presenta una mejor aproximación al punto de preconsolidación que el método de Pacheco Silva.
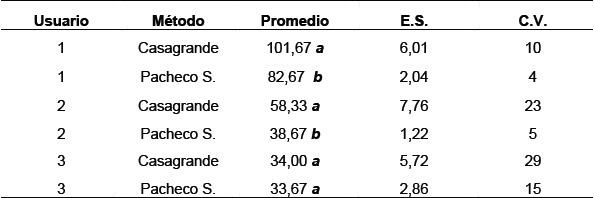 |
Letras
distintas indican diferencias estadísticamente significativas entre los
métodos usados por distintos usuarios según prueba de Tukey (p ≤
0,05). E.S.: error estándar (n:12); C.V. Coeficiente de variación. |
Relación entre métodos de determinación de capacidad de soporte y la resistencia a la penetración.
Con el fin de definir si los resultados que arrojan ambos métodos se relacionan con otras propiedades físico-mecánicas de suelo, se determinó la relación entre la resistencia a la penetración determinada en terreno y la capacidad de soporte determinada en una escala gráfica de 1:1 (Figura 7). Ambos métodos demostraron una relación estadísticamente significativa con la resistencia a la penetración, donde se puede apreciar que al aumentar ésta refleja que el suelo es más estable mecánicamente (aumenta su capacidad de soporte). A resultados similares llego Ellies y Contreras (1997) en suelos similares al del presente trabajo.
CONCLUSIONES
Los métodos analizados se relacionan de muy buena forma cuando son comparados en una escala gráfica de 1:1, presentando el método de Pacheco Silva valores levemente inferiores al de Casagrande. Al evaluar el efecto de distintas estrategias de mejoramiento de una pradera degradada, ambos métodos entregan resultados consistentes.
Matemáticamente, el método de Casagrande es una mejor aproximación del punto de inflexión entre la deformación elástica y plástica. Sin embargo, su determinación es más subjetiva y presentó dependencia de la escala a la cual está siendo evaluada. Cuando el gráfico presenta un ancho mayor al alto, la capacidad de soporte tiende a sobreestimarse y cuando el ancho es menor que el alto este valor se subestima. Esta situación no se presentó en el método de Pacheco Silva, por lo que se puede afirmar que no depende de la escala a la cual está siendo evaluado.
El método de Casagrande resultó presentar mayor variabilidad en su cálculo por distintos usuarios en relación al método de Pacheco Silva. Es así que este último resultó ser de más fácil y rápida determinación, ya que no depende de una interpretación subjetiva ni de la escala a la cual está siendo evaluado.
La capacidad de soporte determinada por ambos métodos aumenta con el incremento de la resistencia a la penetración, no presentándose mayores diferencias entre uno y otro método de determinación de la capacidad de soporte.
AGRADECIMIENTOS
El presente estudio fue financiado por el proyecto SOPROLE “Evaluación de la sustentabilidad de estrategias utilizadas para el mejoramiento de praderas degradadas” (código 160306-02/EN).
NOTAS
4 PAYAHUALA, H. Profesor de estado en matemática, Magíster en matemáticas. Comunicación personal 21 diciembre de 2009.
BIBLIOGRAFÍA.
ALFARO, M.; SALAZAR, F. 2008. Producción animal y contaminación difusa en un suelo volcánico. J. Soil Sc. Plant Nutr. 8: 1-8.
ANGULO-JARAMILLO, R.; MORENO, F.; CLOTHIER, B.E.; THONY, J.L., VACHAUD, G.; FERNANDEZ-BOY, E.; CAYUELA, J.A. 1997. Seasonal variation of hydraulic properties of soils measured using a tension disk infiltrometer. Soil Science Society of America Journal 61: 27-32.
BERRY P.; REID D. 1993. Mecánica de suelos. Santafé de Bogotá, Colombia, Mc Graw Hill. 415 p.
CASAGRANDE, A. 1936. Characteristics of cohesive soils affecting the stability of slopes and Earth fill. J. Boston Soc. Civil Eng. 23: 13-32.
CENTRO DE INFORMACIÓN DE RECURSOS NATURALES (CIREN). 2003. Descripciones de suelos materiales y símbolos. Estudio agrológico X Región. Santiago.412 p.
CLEMENTINO, R. 2005. Discussion of “An oedometer test study on the preconsolidation stress of glaciomarine clays”. Can. Geotech. J. 42: 972-974.
DEC, D.; DÖRNER, J.; HORN, R. 2009. Effect of soil management on soil thermal properties. Revista de la Ciencia del Suelo y Nutrición Vegetal 9: 26-39.
DIAS JUNIOR, M.S.; PIERCE, F.J. 1995. A simple procedure for estimating preconsolidation pressure from soil compression curves. Soil Technology 8: 139-151.
DÖRNER, J.; HORN, R. 2006. Anisotropy of pore functions in structured Stagnic Luvisols in the weichselian moraine region in N Germany. J. Plant Nutr. Soil Sci. 169: 213-220.
DÖRNER, J.; DEC, D. 2008. Efecto de la estructura sobre el movimiento de agua en una catena de suelos. Agro Sur 36: 45-52.
DÖRNER, J., DEC, D., PENG, X., HORN, R. 2009. Change of shrinkage behavior of an Andisol in southern Chile: Effects of land use and wetting/ drying cycles. Soil and Tillage Res. (In press doi:10.1016/j.still.2009.09.013).
ELLIES, A. 1988. Mechanical consolidation in volcanic ash soils. In: Dreschner, J., Horn, R., de Boodt, M. (eds.). Impact of water and external forces on soil structure. Catena Supplement 11: 87-92.
ELLIES, A.; CONTRERAS, C. 1997. Modificaciones estructurales de un Palehumult sometido distintos manejos. Agricultura Técnica 57: 15-21.
GAVANDE, S. 1972. Física de suelos, principios y aplicaciones. México. Limusa. 351 p.
GROZIC, J.; LUNNE, T.; PANDE, S. 2005. Reply to the discussion by Clementino on “An oedometer test study on the preconsolidation stress of glaciomarine clays”. Can. Geotech. 42: 975–976.
HORN, R. 1981. Eine methode zur Ermittlung der Druckbelastung von böden anhand von Drucksetzungsversuchen. Z.F. Kulturtechnik und Flurber 22: 20-26.
HORN, R.; BAUGARTL, T.; KAYSER, R.; BAASCH, S. 1995. Effect of aggregate strength on strength and stress distribution in structured soils. In: Hartge, K.H.; Steward, B. A. (Eds.). Soil structure. Its development and functions. Advances in Soil Science. pp 31-52.
HORN, R.; SIMOTA, C.; FLEIGE, H.; DEXTER, A.; RAJKAI, K.; DE LA ROSA, D. 2002. Prediction of soil strength of arable soils and stress dependent changes in ecological properties based on maps. Z.Pfanzenernährung und Bodenkunde 165: 235–240.
KÉZDI, A. 1980. Handbook of soil mechanics. Vol. 2. Soil Testing. Elsevier. Amsterdam, The Netherlands. 258 p.
ORTIGAO, J. 1995. Soil mechanics in the light of critical state theories. Rotterdam.AA Balkema. 299 p.
PACHECO SILVA, F. 1970. A new graphical construction for determination of the pre-consolidation stress of a soil sample. In: Proceedings of the 4th Brazilian Conference on Soil Mechanics and Foundation Engineering, Río de Janeiro, Brazil. Vol. 2, No. 1, pp. 225-232.
SEGUEL, O. 2006. Influencia del potencial mátrico en la generación de estructura y resistencia mecánica de suelos derivados de materiales volcánicos. Tesis Doctoral. Universidad Austral de Chile. Facultad de Ciencias Agrarias. Doctorado en Ciencias Agrarias.
SEGUEL, O.; ORELLANA, I. 2008. Relación entre las propiedades mecánicas de suelo y los procesos de génesis e intensidad de uso. Agro Sur 36: 82-92.
TABOADA, M. 2007. Efecto del pisoteo y pastoreo animal sobre suelos en siembra directa. 4º Simposio de ganadería en siembra directa. Aapresid, Potrero de los Funes, San Luis. pp 71-83.
TERZAGHI, K.; PECK, 1963. Mecánica de suelos en la ingeniería práctica. Buenos Aires, Ateneo. 633 p.
Recepción Originales: 18 de agosto 2009