Estudios Pedagógicos
XXXI, N° 1,
2005, pp. 97-112
DOI: 10.4067/S0718-07052005000100006
INVESTIGACIONES
ATTITUDES TOWARD MATHEMATICS AND ACADEMIC PERFORMANCE AMONG CHILEAN 8TH GRADERS
Actitudes hacia las matemáticas y el rendimiento académico entre estudiantes de Octavo Básico
María José Ramírez, Ph.D.
TIMSS & PIRLS International Study Center, Boston College, 188 Beacon Street, Chestnut Hill, MA 02467, USA. ramiremb@bc.edu ; ramirezmjose@yahoo.com
Abstract
Using data from the 1999 Trends in International Mathematics and Science Study (TIMSS), this study reveals that the Chilean students like and value mathematics, but have an inflated self-perception of their mathematic competence. Hierarchical linear models were used to predict mathematic achievement both at the student-within-class and class levels. At both levels, students' perceived difficulty of doing mathematics, expectations for further education, and beliefs regarding the causes of their mathematics outcomes were significant predictors of achievement. However, classes having more students liking mathematics had significantly lower mean scores. This later result is interpreted as the consequence of the more demanding curriculum and tougher grading standards used in higher performing classes.
Key words: mathematics achievement, student attitudes, middle school students, Chile.
Resumen
Usando datos del Estudio Internacional de Tendencias en Matemáticas y Ciencias de 1999, este trabajo muestra que los alumnos chilenos disfrutan las matemáticas y las encuentran importantes. Al mismo tiempo, los jóvenes tienen una inflada autopercepción de sus habilidades matemáticas. En este estudio se usaron modelos lineares jerárquicos para predecir rendimiento en matemáticas a nivel de alumnos y a nivel de las salas de clases. En ambos niveles, fue significativo el efecto de dificultad de hacer matemáticas, creencias en torno a las causas del desempeño en esta disciplina y expectativas de educación futura. Paradójicamente, en los cursos donde los alumnos reportan disfrutar más las matemáticas se observa un peor rendimiento promedio que en los cursos donde los alumnos no reportan una actitud tan positiva. Estos últimos resultados se interpretan como la consecuencia de la mayor exigencia curricular y de los más altos estándares de evaluación a los que son sometidos los alumnos de cursos con alto rendimiento promedio en matemáticas.
Palabras clave: rendimiento en matemáticas, actitudes de los alumnos, segundo ciclo de educación primaria, Chile.
In Chile, the debate about how to improve academic achievement usually points to structural factors such as teacher education programs, school resources, or curricula. However, little attention has been given to students' characteristics such as how much they like mathematics, how important they think it is, how difficult they perceive it is to do well in mathematics, and what factors they believe affect their mathematics performance. By the same token, little is known about students' aspirations for further education: Do Chilean students look forward to finishing their secondary school or do they plan to enter the university?
Students' opinions and beliefs regarding mathematics, how much they like and value it, and what they forecast for their own future education can all be understood as different facets of students' attitudes toward mathematics. An attitude is an internal disposition to evaluate in positive or negative terms an object, which is accompanied by affective, cognitive, and behavioral responses (for a detailed discussion, see Aiken, 2002). The study of attitudes toward mathematics is justified from at least three standpoints. First, the development of positive attitudes is a goal for many educational systems; they are seen as a requisite for students' academic engagement and to boost learning. Second, attitudes are learned predispositions that reflect the school ethos and the wider social context in which mathematics instruction occurs. As such, attitudes can be influenced by policy interventions. Third, the literature has suggested that there is a positive relationship between attitudes toward mathematics and academic competence.
The study of attitudes in the school setting has several complications, though. Because of the different facets of the attitude construct, what is meant by attitudes toward mathematics varies from one study to the other. Moreover, it is common to find studies that do not use the term attitudes, but whose focus lay in one or more of its facets (e.g., academic self-perception, locus of control). The unit of analysis is another complication in the study of attitudes. Relationships that may hold true at the student level may not be of the same nature and strength at the school or classroom level.
From the Trends in International Mathematics and Science Study (TIMSS) 1995 there is evidence that the majority of 8th graders around the world liked mathematics, thought it was important for them to do well in this subject, thought it was not boring, and did not find it easy (Kifer, 2002). In school effectiveness studies, expectations for further education had been reported as a strong predictor of school mean achievement across the countries (Martin, Mullis, Gregory, Hoyle, & Shen, 2000). In South Africa, students with higher self-concepts (i.e., who thought that doing well in mathematics was not so difficult) and who valued the importance of mathematics, were more likely than their peers with low self-concepts to attain higher mathematics performance (Howie, 2002).
Using data from the Chilean national assessment system, SIMCE, Ramírez (2003) found that 4th graders with more positive attitudes toward their studies (as reported by their parents) attained substantially higher mathematics scores than students with more negative attitudes. By the same token, the more the parents expected their children to study in the university, the higher the child mathematics performance.
In Israel, Nasser and Birenbaum (2004) studied the relationship between mathematics achievement and some learner-related variables, including self-efficacy, beliefs regarding knowledge, and attitudes toward mathematics. The authors conducted their study in two samples of 8th graders: Arabs and Jews. They reported that in both groups the strongest predictor of mathematics achievement was students' beliefs regarding their performance capabilities in mathematics (self-efficacy). The better the students evaluated themselves in doing mathematics, the higher their academic performance.
These authors operationalized attitudes towards mathematics as encompassing how much the students liked mathematics, how difficult they found it, and how important they thought it was. The relationship between mathematics achievement and attitudes was not so clear. They found that attitudes had minor and insignificant effects on mathematics achievement of Jewish children, while it had a modest but significant effect on the Arabs. Arab students reporting more positive attitudes toward mathematics attained a higher performance than those reporting more negative attitudes. Interestingly, while the Jewish students outperformed their Arab peers in mathematics, the latter reported more positive attitudes toward this subject.
Shen and Pedulla (2000) reported that more students from lower performing countries (or systems) have more positive attitudes toward mathematics: they found it easier and perceived themselves as more capable of doing well in this subject. These authors interpreted their findings as the consequence of more demanding curricula and high standards used in high achievement countries, which may lead the students to see mathematics as a harder topic, and themselves as not so strong in doing mathematics.
Benham (1995) reviewed studies relating students' self-perceptions and academic achievement. When students believed that their academic performance was the consequence of their own actions (e.g., studying hard, perseverance, motivation) rather than the consequence of factors out of their control (e.g., good luck, innate ability), they had better academic performance. In the literature, the former are said to have an internal locus of control, while the latter have an external one. Stemler (2001) provided further evidence of the importance of the students developing an internal locus of control. From an analysis of 4th grade TIMSS 1995 data from 14 countries, he concluded, "effective schools tend to have a student body who is able to see a connection between hard work, ability, and achievement and are less likely to attribute achievement to factors such as luck" (p. 145).
In education, it is a fact that the socio-economic background of the students' families plays an important role in explaining academic achievement. Poorer students attain substantially lower achievement levels than their peers from more economically advantaged backgrounds. In Chile, the educational system is highly stratified by social class. Broadly speaking, public schools serve the poorer families, private-subsidized schools serve the middle-class, and the elite-paid schools serve the richer families. Not surprisingly, the public system has consistently gotten lower scores in standardized achievement tests (Ministerio de Educación [Mineduc], 2001). In this scenario, attempts to account for the mean achievement differences among classes from different schools should consider the effect of the socio-economic level of the communities served by the schools. Within the Chilean schools, though, students within communities are homogeneous in their socio-economic background. Hence, this factor cannot account for the large variations in achievement observed within the classes. In this context, students' attitudes toward mathematics may account for an important proportion of the achievement variation among classmates.
The purpose of this study is to know the attitudes of Chilean 8th graders toward mathematics, and the relationship between students' attitudes and mathematics achievement. More specifically, this study aims to describe the students in terms of how much they like and value mathematics, how difficult they think it is do well in mathematics, how much influence they think good luck and innate talent have on their mathematics outcomes, and how far in their studies they plan to go. Because the results may vary substantially depending on the unit of analysis, this study distinguished between a student-within-class and a class level.
The following research questions guided the analyses:
| 1. | Within the classes, how much of the variation in mathematics achievement can be predicted by the students' attitudes toward mathematics? |
| 2. | Among the classes, how much of the variation in mean mathematics achievement can be predicted by the aggregated students' attitudes toward mathematics, once socio-economic background is held constant? |
My interest in doing this study comes from the firm belief that structural changes are a necessary but not sufficient condition to reach the goals set by an ambitious educational reform in Chile. After a decade of improvements in areas like libraries, curriculum, and working conditions for teachers, there is no evidence of improved students' achievement. Perhaps it is time to put more emphasis on the students themselves and on how their characteristics may be affecting their own learning processes. The study of students' attitudes toward mathematics and their link to academic performance is definitely an aspect worth examining.
METHOD
Source of Information. Data from the 1999 Trends in International Mathematics and Science Study (TIMSS) was the main source of information for this study. In Chile, a nationally representative sample of 5,907 eighth graders nested in 185 classes each from different schools took the TIMSS test at the end of the 1998 school year (November). The students answered a questionnaire providing background information, including their attitudes and beliefs about mathematics and the resources they had at home. All this information is in the TIMSS 1999 International Database (2000).
Predictor Variables. The TIMSS Students' Questionnaire was scanned in search of questions related to students' attitudes toward mathematics. In a preliminary round, 24 questions were selected. Principal component analysis (PCA) was used to identify underlying factors that could account for the shared variance among the items. Different selection criteria and rotation techniques were tested. The results suggested the presence of three factors. The first one, named importance of luck and talent in doing mathematics, accounted for the variation of items like "to do well in mathematics at school you need good luck," and "to do well in mathematics at school you need lots of innate talent." The second factor, labeled importance of mathematics, related to items like "I think it is important to do well in mathematics at school" and "mathematics is important to everyone's life." The third factor encompassed both items related to liking mathematics "I enjoy learning mathematics" and items related to the difficulty of doing mathematics "mathematics is an easy subject." These three factors accounted for 52% of the total item variance. Since the third factor referred to two clearly differentiated concepts, its items were split accordingly in two factors. The questionnaire also included one item related to students' expectations for further education; this item was used as indicator of a fifth factor.
For the multi-items factors, indices that combined information from several questions were created with the purpose to increase the validity and reliability of the measures, and also to allow for data reduction. Items conceptually related to the constructs, with factor loadings r > .25, item-total correlations rb > .32, and related to the outcome according to expectations, were selected as indicators of the four multi-items factors. As a result of this process, 18 questions were selected for the final analyses.
The indices were computed averaging the points associated with each response option. Before averaging, all the questions were scaled in the same direction. In case of missing data, the index value was computed based on the valid responses to the other source questions. This allowed maximizing the number of valid cases to be used in the analyses. For the single-item factor educational expectations, mean imputation was used to treat both missing cases and I don't know responses. In this study, the final analyses were based on data from all the sampled schools and 98% of the sampled students (N = 5,789).
A socio-economic index (SEI) was used as an indicator of the average cultural and economic capital of the students' families. This index was computed averaging the score points associated with three questions: "How far in school did your mother and father go?," "about how many books are there in your home?" and "do you have any of these items at your home?" (e.g., computer, refrigerator).
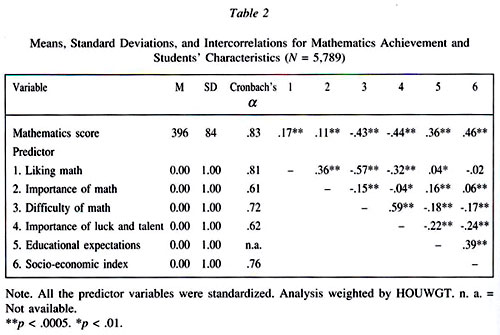
The mean, standard deviation, and internal consistency (Cronbach's a) for mathematics achievement (outcome), liking mathematics, importance of mathematics, difficulty of doing mathematics, importance of luck and talent, students' expectations for further education, and the socio-economic index are presented in Table 2. While reliability is not high, it is important to bear in mind the reduced number of items used as indicators of each index.
Despite the fact that all the factors were significantly correlated with the outcome (p < .0005), these correlations were of low to moderate magnitude. The strongest correlation was between mathematics scores and the socio-economic index (r = .46). Students from more economically advantaged families were more likely to attain higher scores than their mates from lower income backgrounds. A negative correlation was observed between importance of luck and talent and the outcome (r = -44). The more the students thought that to do well in mathematics they need good luck and innate talent, the lower their performance. By the same token, students who perceived that it was difficult to do mathematics were more likely to have lower achievement scores (r = -.43), as compared to their mates perceiving that doing well in mathematics was not so difficult. The other variables had a positive relationship with the outcome: the more the students liked mathematics, thought it was important, and the higher their educational aspirations, the higher their mathematics scores.
The inter-correlations between the predictors were of low to moderate magnitude; however, they were significant in all but one case at p < .01. The more the students liked mathematics, the less difficult they found it (r = -.57), and the less difficult doing math was perceived, the less the students relied on luck and talent (r = .59). Students from more privileged socio-economic backgrounds reported higher educational aspirations (r = .39) and less reliance on luck and talent (r = -.24).
PROCEDURES
In the TIMSS sampling design, all the students from one intact class participated in the study, and only one class per school was sampled. Because of this nested design, the final sampling units (students) were not independent one of each other, and so hierarchical linear models (HLM) were statistically appropriate to model mathematics scores. This technique also presented the advantage of providing a more comprehensive picture of the strength of the relationship between factors and achievement at different levels of analysis.
At the student-within-class level, the sub-model predicted differences in mathematics scores among classmates who shared the same classes and schools, and students' attitudes variables were used as predictors. At the class level, the sub-models predicted differences in mean classes scores, and the aggregated students' characteristics were used as predictors. The mathematics scores (five plausible values) were used as the outcome variable, while the socio-economic index served as a covariate at the class level.
The following equations specify the sub-models used in the hierarchical linear models. The unconditional model informed about the proportion of variance that lay among classes and within classes. In this model no predictors were entered at either level (Equations 1 and 2):
| (1) | ||
| (2) | ||
 |
In the socio-economic sub-model, the aggregated socio-economic index was entered as predictors at the class level (Equations 3):
| (3) | ||
 |
In the expanded sub-models, the attitude factors were entered as predictors at both levels, and the socio-economic index was entered as a covariate at the class level only (Equations 4 and 5):
| (4) | ||
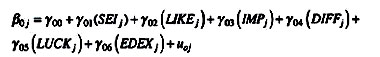 |
(5) | |
 |
RESULTS
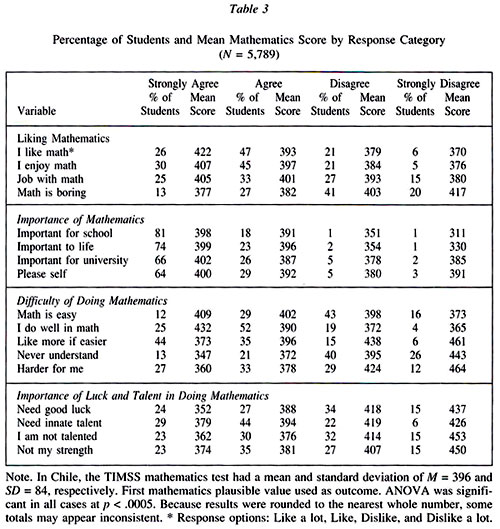
Table 3 shows the questions related to attitudes toward mathematics used in this study, together with the percentage of students by response category and their mean mathematics score. In all the cases, a one-way analysis of variance (ANOVA) showed that mathematics achievement varied significantly depending upon the response categories of the questions (p < .0005). Students attained relatively higher achievement when they agreed with statements emphasizing that mathematics is easy, important, and enjoyable and when they disagreed with statements emphasizing the importance of good luck and innate talent.
Some noteworthy results were that 51% of the Chilean students endorsed (agreed or strongly agreed) the statement "to do well in mathematics you need good luck," and 73% did so with "to do well in mathematics you need lots of innate talent." Despite the poor performance of the Chilean students in the TIMSS mathematics test1, up to 77% of the students endorsed the statement "I usually do well in mathematics," and 41% did so with "mathematics is an easy subject."
The vast majority of the students (81%) strongly agreed with "I think it is important to do well in mathematics at school," and less than 10% disagreed or strongly disagreed with statements related to the importance of mathematics. Three-fourths of the students (75%) endorsed the statement "I enjoy learning mathematics," and 26% reported that they liked mathematics a lot.
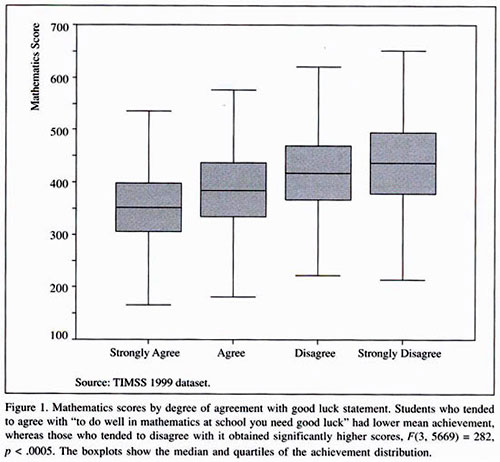
Figure 1 represents the relationship between mathematics scores and the degree of agreement with "to do well in mathematics you need good luck." There is a monotonic relationship between the variables: increases in one are associated with increases in the other. Students who strongly disagreed with the statement "to do well in mathematics you need good luck" scored 85 points more (one standard deviation) than their peers who strongly agreed with it.
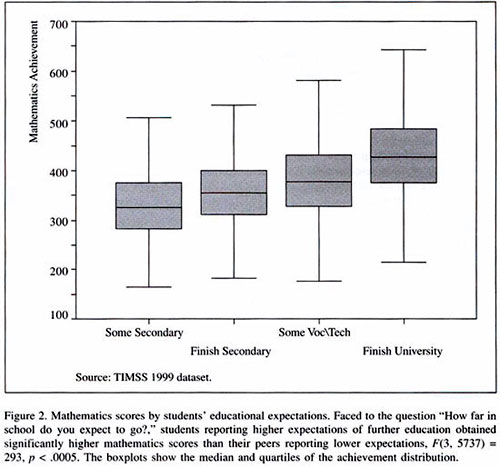
Figure 2 shows how mathematics scores increased for students with higher expectations for further education (not shown in previous table). Students aspiring to finish the university (43%) averaged 429 points on the mathematics test, compared to the 355 points obtained by their classmates aspiring to finish secondary school only (15%).
HOW MUCH ACHIEVEMENT VARIANCE CAN BE PREDICTED BY STUDENTS' ATTITUDES TOWARD MATHEMATICS?
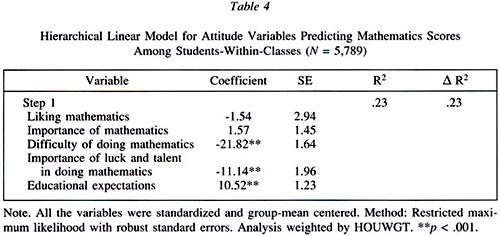
The HLM unconditional model indicated that 61% of the variations in mathematics score lay within the classes while 39% lay among the classes from different schools. Table 4 shows the results of the hierarchical linear models at the student-within-class level; in this model, the five attitudes factors were entered as predictors. This model accounted for 23% of the outcome variance that lay within the classes.
Significant predictors were difficulty of doing mathematics, importance of luck and talent, and expectations for further education. Within the classes, students reporting that doing mathematics was more difficult had lower scores than their mates reporting that this subject was not so difficult (b = -21.82, p < .001), beyond the effect of the other variables in the model. Students relying more heavily on luck and innate talent to do well in mathematics also had significantly lower scores than their classmates reporting less reliance on them (b = -11.14, p < .001), after controlling statistically for the other variables in the model. Students with higher expectations for further education attained significantly higher achievement scores than their classmates with lower expectations (b = 10.52, p < .001); other variables held constant.
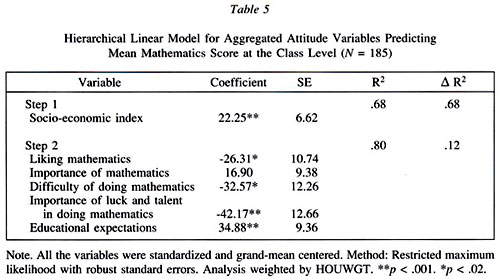
At the class level (Table 5), the socio-economic index was entered alone in Step 1; this control variable was highly significant, explaining up to 68% of the mean score differences among the classes. Classes with more students from economically advantaged homes had higher mean scores than classes with less advantaged students.
In Step 2, another sub-model encompassing both the socio-economic index and the aggregated attitudes variables was tested. This sub-model accounted for 80% of the outcome variance (i.e., 12 percentage points more than the previous model). With the exemption of importance of mathematics, all the predictors made a significant partial contribution to the outcome variance (p < .02).
Liking mathematics made a negative partial contribution to the outcome (b = -26.31, p < .02). Classes with more students liking mathematics attained lower mean achievement than classes with less students liking this subject. When in a class there were more students who found mathematics difficult, the mean class achievement was lower (b = -32.57, p < .02). When in a class there were more students who relied on having good luck or innate talent to do well in mathematics, the mean class score was significantly lower, net the effect of the other variables in the model (b = -42.17, p < .02). When classes had more students with higher expectations for further education, the mean class achievement was higher, compared to classes having fewer students with high educational aspirations (b = 34.88, p < .001); other variables held constant.
DISCUSSION
Consistent with the international evidence (Kifer, 2002), the Chilean 8th graders have very positive views of mathematics: three-fourths report liking or enjoying this subject, and more than half would like a job involving mathematics in the future. Almost all the students think that it is important to do well in mathematics, and over 90% feel external pressures (e.g., university) that push them further to do well in this subject. In a country where only an elite has access to the university, an impressive 40% of the 8th graders aspire to graduate from university.
Nevertheless, less auspicious results arise from the analysis of other aspects of students' attitudes toward mathematics. Half of the students think that to do well in mathematics they need good luck, while 40% think that they need an innate talent that they do not have. It is clear that these students do not feel in control of their own learning processes. Consequently, it is hard for them to see a connection between their own efforts and motivation to do well and their academic performance. These findings suggest failures in molding a more active role for the students in their own learning processes.
In Chile, there is a recognized gap between the objectives stated in the national curriculum and what the students know and are able to do (Mineduc, 2001). This country was also among the lowest performing in TIMSS 1999 (35th out of 38 countries) (Mullis et al., 2000). Nevertheless, 41% of the Chilean students think that mathematics is an easy subject and, surprisingly enough, over three-fourths report that they usually do well in this subject. It is clear that the Chilean students have an extremely high and distorted self-perception of their own mathematics knowledge and skills.
Mathematics difficulty and self-competence are mainly a function of the difficulty level of the topics covered in classes and, most importantly, of the grades the students get in classroom evaluations. There is evidence that the Chilean teachers cover little advanced mathematics topics in the 8th grade (e.g., algebra, geometry), preferring to emphasize basic contents like fractions and numbers sense (Ramírez, 2004, in press). It may be the case that the students perceive mathematics as an easy subject because they see variations of the same topics during the school year. If this is the case, teachers should consider covering more advanced and challenging mathematics topics in classes.
It is highly likely that the students use their own grades in judging how well they do in mathematics. In Chile, it is well known that the grades do not reflect the curricular standards; grade inflation is a pervasive problem (Riveros, 2004). Teachers "lower the bar" to the average student, and grade them based on this relative standard. Too many schools work in a culture of low academic standards and poor expectations for their students. This lack of rigor is perceived as one of the main problems of the Chilean education system (Arancibia, 1994). This situation should lead to a serious review of the teachers' assessment and evaluation practices. If the students are not corrected in their errors, and if they do not know their real level of performance, it will be difficult to put more pressure on them to study harder. By the same token, it will be difficult to involve parents in supporting their children's learning.
The research questions of this study asked how well the students' attitudes toward mathematics predict the achievement differences among classmates, and how well they predict the achievement differences among the classes. Within the classes, the students' attitudes accounted for almost one-fourth (23%) of the variations in achievement, which is a substantial amount. Students who rely less on factors out of their reach (e.g., good luck, innate talent), report little difficulty with mathematics, and expect to finish the university, attain significantly higher achievement than their classmates who rely more heavily on luck and talent, think that doing mathematics is harder, and do not aspire to finish the university.
At the class level, students' attitudes toward mathematics accounted for one-tenth of the variations in mean class achievement, beyond the effect of socio-economic level. Classes having more students expecting to finish the university, less students perceiving that doing well in mathematics is difficult, and less students who rely on good luck and innate talent to do well, attain higher mean achievement than classes with less students planning to go into the university, more students perceiving that doing mathematics is hard, and more students relying on good luck and innate talent.
These findings can be interpreted as a positive cycle where expectations for further education, perceived self-efficacy of doing mathematics, and mathematics achievement have mutual influences one on each other. The findings also suggest the importance of fostering a perception that students' academic outcomes depend to a greater extend on students' own effort and motivation to do well, and less on factors out of their control, such as good luck or innate ability. Timely feedback, assessments that reflect the real students' performance levels, and opportunities to compare previous to current performance levels are strategies that may help the students to change their beliefs regarding the causes of their mathematics outcomes (for a detailed discussion, see Benham, 1995).
Contrary to the popular belief, liking or valuing mathematics has little further to do with achievement, when analyzed at the student level. This assertion makes sense considering that almost all the Chilean students like and value mathematics. A measurement problem may be obscuring the link of these factors with achievement. It is perhaps the case that students have a tendency to answer according to what is socially accepted and valued (social desirability), hence that the vast majority of the students report liking and valuing mathematics. Maholmes (2001) speculates on this and other plausible explanations of why minority students in the United States report liking mathematics.
Interestingly, while liking mathematics was not a significant predictor of achievement within the classes, it has a significant and negative relationship with the outcome at the class level: classes with higher mean achievement have fewer students who like mathematics. As already suggested by other authors (Shen & Pedulla, 2000), it may be the case that students in higher performing classes do not like mathematics as a consequence of the more demanding curriculum and stringent grading policies. On the contrary, less demanding classes may be promoting positive affects at the cost of higher achievement; thus, reaching learning levels far below the curricular expectations for the grade.
It is reasonable to conclude that, in Chile, it is important to change some students' beliefs regarding the nature of learning and the factors that affect it. The development of a more realistic appreciation of the students' own capacities to do well in mathematics also seems desirable. It is likely that changing students' self-appreciation will require improving teachers' grading standards. These findings are encouraging since they point toward variables that are relatively independent of the strong effect of socio-economic level. However, they are also challenging since changing beliefs, opinions, and evaluation standards (toward self and others) imply changing some cultural patterns deeply rooted in the Chilean society.
Notes
1 Chile ranked 35th out of 38 countries participating in the assessment. Only half of the Chilean 8th graders were able to do basic computations with whole numbers (add, subtract, and round). According to the Chilean curriculum, students should have mastered these skills in the first cycle of primary education (grades 1-4).
References
Aiken, L. R. (2002). Attitudes and related psychosocial constructs: Theory, assessment, and research. Thousand Oaks, CA: Sage Publications.
Arancibia, V. (1994). La educación en Chile: percepciones de la opinión pública y de expertos [Education in Chile: opinions from the broad public and experts]. Estudios Públicos 54 125-151.
Benham, M. (1995). Fostering self-motivated behavior, personal responsibility, and internal locus of control in the school setting. Retrieved from ERIC ED 386 621.
Howie, S. (2002). English language proficiency and contextual factors influencing mathematics achievement of secondary school pupils in South Africa. Enschede, The Netherlands: Print Partners Ipskamp.
Kifer, E. W. (2002). Students' attitudes and perceptions. In D. F. Robitaille & A. E. Beaton (eds.). Secondary analysis of the TIMSS data. Dordrecht, The Netherlands: Kluwer Academic Publishers.
Maholmes, V. (2001). Revising stereotype threats: examining minority students' attitudes toward learning mathematics and science. Race, Gender, and Class, 8. 1: 8.
Martin, M. O., I. V. S. Mullis, K. D. Gregory, C. Hoyle, C. Shen, C. (2000). Effective schools in science and mathematics: IEA's Third International Mathematics and Science Study. Chestnut Hill, MA: International Study Center Lynch School of Education Boston College.
Martin, M. O., K. D. Gregory, S. E. Stemler (2000). TIMSS 1999 technical report: IEA's repeat of the Third International Mathematics and Science Study at the eighth grade. Chestnut Hill, MA: International Study Center Lynch School of Education Boston College.
Ministerio de Educación (Mineduc). (2001). Informe de resultados 8th básico SIMCE 2000 (SIMCE 2000 Report for the 8th grade). Santiago: Chile: Ministerio de Educación.
Mullis, I. V. S., M. O. Martin, E. J. Gonzalez, K. D. Gregory, R. A. Garden, K. M. O'Connor, S. J. Chrostowski, T.A. Smith (2000). TIMSS 1999 international mathematics report: Findings from IEA's repeat of the Third International Mathematics and Science Study at the eighth grade. Chestnut Hill, MA: International Study Center, Lynch School of Education, Boston College.
Nasser, F., M. Birenbaum (2004). Modeling mathematics achievement of Jewish and Arab eighth graders in Israel: The effect of learner-related variables. Boston College: Unpublished manuscript.
Ramírez, M. J. (2003). The distribution of mathematics knowledge among Chilean fourth graders and related explanatory factors. EducarChile. Retrieved May 2003 from: http://200.68.0.6/medios/20030604142903.pdf
Ramírez, M. J. (2004). Understanding the low mathematics achievement of Chilean students: a cross-national analysis using TIMSS data. Boston College: Unpublished doctoral dissertation.
Ramírez, M. J. (in press). Factors that affect mathematics achievement among Chilean 8th graders. In S. J. Howie & T. Plomp (eds.). Context of learning mathematics and science: Lessons learned from TIMSS. The Netherlands: Routledge Falmer.
Riveros, L. A. (2004, September 22). Inflación de notas [Grade inflation]. Diario Estrategia. Retrieved October 15, 2004, from http://www.uchile.cl/acera/rectoria/publicaciones/opinion/22092004
Shen, C., J. J. Pedulla (2003). The relationship between students' achievement and their self-perception of competence and rigour of mathematics and science: a cross-national analysis. Assessment in Education: Principles, Policy and Practice 7(2). Retrieved December 23, 2003. from http://metalib.bc.edu/login?url=http://www.ingentaselect.com/rpsv/cw/carfax/0969594x/contp1.htm
Stemler, S. E. (2001). Examining school effectiveness at the fourth grade: a hierarchical analysis of the third international mathematics and science study (TIMSS) (Doctoral dissertation, Boston College, 2001). Dissertation Abstracts International, 62, 03A.
TIMSS 1999 International Database 1999 Assessment Data [CD-ROM]. (2000). Chestnut Hill, MA: International Study Center Lynch School of Education Boston College.