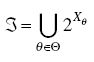
Estudios Pedagógicos XXXVI, Nº 2: 51-61, 2010
INVESTIGACIONES
UNA DIDACTICA DEL SABER: UN CAMINO HACIA LA OPTIMIZACION DE LAS TRANSPOSICIONES DIDACTICAS
Didactics on Knowledge: a Road to the Optimization of Didactic Transpositions
Uma didática do saber: um caminho à optimização das transposições didáticas
Eduardo Cabrera *, José González *, Eduardo Montenegro *, Alejandro Nettle *
Lab[e]saM
Departamento de Matemática & Física / Facultad de Ciencias Naturales
& Exactas. Universidad de Playa Ancha Valparaíso-Chile - E-mail:
labesam.upla@gmail.com.
* Equipo Laboratorio [EXPERIMENTAL] de Saberes Matemáticos
(i.e., Equipo Lab[e]saM ) inserto en el Departamento de Matemática & Física,
Facultad de Ciencias Naturales & Exactas, Universidad de Playa
Ancha / Valparaíso, CHILE.
RESUMEN
Preocupados por la educación de calidad, y dentro del marco de la Teoría de las Situaciones Didácticas (Brousseau, 2004), y particularmente en la aproximación antropológica propuesta por Yves Chevallard (1991)1, en este trabajo se presenta una herramienta que, en esta primera etapa, aspira a optimizar el proceso de transposición didáctica, a través de la definición de una distancia entre el saber a enseñar y el saber aprendido (Mabille & Albert, 1994)2, postulando el saber como un ente multidimensional y cada una de estas dimensiones independientes entre sí. Por otro lado, la definición de distancia se estructura bajo una concepción estocástica, utilizando la función logística para modelar la probabilidad de emitir una respuesta correcta a un estímulo en función del saber aprendido.
Palabras clave: Saber sabio, saber a enseñar, saber aprendido, transposición didáctica, distancia, función logística.
ABSTRACT
Worried about the quality of education and within the framework of the Theory of Didactical Situations in Mathematics (Brousseau, 1998), and particularly in the anthropological approach proposed by Yves Chevallard (1991), this paper presents a tool that, in its first place, aims at optimizing the process of didactic transpositions, through the definition of a distance between the knowing how to teach and the knowledge learned (Mabille & Albert, 1994), by proposing the knowledge to be a multidimensional being and each one of these dimensions to be independent from each other. On the other hand, the definition of distance is structured according to a stochastic conception, using the logistic function to model the probability of emitting a correct answer to stimulus acting on the knowledge learned.
Key words: Wise knowledge, knowing how to teach, knowledge learned, didactic transposition, distance and logistic function.
RESUMO
Preocupado com a educação de qualidade, e no âmbito da Teoria das Situações Didáticas (Brousseau, 2004)3, e em particular na abordagem antropológica proposta por Yves Chevallard (1991)4, este trabalho apresenta uma ferramenta que, nessa primeira fase, visa otimizar o processo da transposição didática, através da definição de uma distância entre o saber ensinar e o conhecimento aprendido (Mabille & Albert, 1994)5, postulando o saber como uma entidade multidimensional e cada uma dessas dimensões sendo independentes umas das outras. Por outro lado, a definição de distância é estruturada sob uma concepção estocástica, utilizando a função logística para modelar a probabilidade de emitir uma resposta correta a um estímulo em termos de conhecimento aprendido.
Palavras-chave: Saber sábio, saber ensenhar, Conhecimento aprendido, transposição didática, distância e função logística.
1. INTRODUCCION
Este trabajo está motivado por una urgente necesidad, del ámbito educacional, de poder desarrollar un sustento conceptual formal respecto de las técnicas evaluativas de los procesos de transposición didáctica (Chevallard, 1991: 45)6. Para ello recurriremos a algunas herramientas estadísticas. En efecto, hoy en día la estadística nos ofrece, en general, dos enfoques para dar tratamiento a la evaluación de contenidos educacionales: la Teoría Clásica de los Test (i.e., TC), que se basa en el Modelo Lineal Clásico, y la Teoría de Respuesta al Item, que está centrada en los ítemes que los caracteriza por medio de relaciones basadas en los modelos de probabilidad tipo Rasch o logístico.
En este trabajo presentamos una propuesta metodológica que aspira a optimizar los procesos de transposición didáctica, iniciando previamente una discusión teórica para concluir un diagrama de relaciones entre los saberes, que nos ayude a visualizar y comprender el sentido de la propuesta, y la manera como ésta opera.
2. EL PROBLEMA DE INVESTIGACIÓN
Nuestro problema de investigación es consecuencia de muchos años de estudios, centrados en la caracterización de transposiciones didácticas y las mejoras en los aprendizajes.
En efecto, el problema se centra en definir una estructura formal de los estatus del saber, y definir una métrica adecuada que mida la distancia entre el saber a enseñar y el saber aprendido como una herramienta para optimizar los procesos de transposiciones didácticas.
3. OBJETIVOS DE LA INVESTIGACIÓN QUE SE PRESENTA
• Proponer un modelo secuencial de los saberes.
• Definir una distancia entre el saber a enseñar y el saber
aprendido.
• Contextualizar la distancia definida para optimizar el proceso
de transposición didáctica.
4. METODOLOGIA DE LA INVESTIGACIÓN
La Teoría de Situaciones Didácticas y la Teoría de Respuesta al Item (i.e., IRT) serán el soporte teórico y andamiaje de nuestra construcción y propuesta.
El saber a enseñar conforma el objeto de diseño de nuestra investigación, pues sobre él se desarrolla el contraste para la cuantificación del saber aprendido, y por lo tanto la evaluación del proceso de transposición didáctica a través de la métrica euclidiana y el método de estimación de máxima verosimilitud bajo la utilización de la IRT.
Lo anterior establecerá las siguientes fases de la investigación:
1. Análisis preliminar,
2. Concepción de la investigación, y
3. Simulaciones.
5. ALGUNOS ANALISIS PRELIMINARES
La mayoría de los atributos físicos resultan directamente medibles, los constructos psicosociales resultan ser conceptualizaciones teóricas que no son accesibles a la medición directa, para los que no existen “Metros” o “Balanzas” diseñadas para medirlos de manera precisa. La actitud hacia el aborto, el nivel de cohesión grupal, el coeficiente intelectual, la postura hacia el consumo de drogas, el grado de liderazgo y muchos otros ejemplos son constructos que deben medirse mediante instrumentos específicamente diseñados: Los test, cuestionarios o inventarios. Nadie dudaría que un metro bien diseñado mide longitud y que lo hace de manera precisa, pero la bondad y precisión de un cuestionario no se puede presuponer; más bien es una cuestión de grado, y siempre susceptibles de mejorar.
En muchos sistemas educativos se da la necesidad de disponer de un mecanismo para evaluar la adquisición de conocimiento de los alumnos, algo fundamental para identificar el éxito o fracaso en el proceso de aprendizaje. Los tests son probablemente hoy en día el modo más habitual de efectuar dicha tarea, pudiendo estar ligado a diferentes contextos educativos.
En la actualidad los estudios se centran en poder determinar y optimizar el grado de estabilidad, precisión o consistencia que manifiesta el test como instrumento de medición del constructo. Es por esto que se han generado nuevas tendencias en el ámbito de los test, de tal manera que el constructo que determina a cada sujeto sea definido con mayor precisión (Cortada de Kohan, N. 2003).
Históricamente, la primera teoría fue la que hoy se conoce como Teoría Clásica de los Test, que surgió a comienzos del siglo XX. Si bien no recibió su forma axiomática hasta mediados de la década de los 60, la TC se fundamenta en el denominado modelo clásico que establece una relación lineal entre el nivel del constructo del examinado y la puntuación obtenida en el test realizado (López, J., Pérez, T. & Armendáriz, A. 2004).
X = V + ε
Este modelo se expresa en términos de la puntuación empírica del test, el elemento central sobre el que gira toda la teoría. Concretamente, se considera que la puntuación empírica del sujeto, esto es, el valor observado en el test, es igual a la suma de dos componentes hipotéticos y desconocidos a priori: la puntuación verdadera o nivel del constructo real del evaluando y un determinado error de medida (Muñiz, J., 1997).
La principal limitación de la TC es que en su contexto las características del test y las del examinado son dependientes, esto es, las mediciones obtenidas dependen por lo general de la naturaleza del test utilizado y, a la inversa, las propiedades de los test dependen de los sujetos a los cuales se aplica. Así, para la TC, el nivel del constructo del alumno se mide mediante el número de respuestas acertadas en el test realizado. Por lo tanto, los resultados estarán siempre relacionados con el test administrado: si las preguntas son difíciles, el nivel del constructo de los examinados resultará ser bajo porque habrá pocos que la respondan correctamente; y viceversa. Así, la dificultad estimada de un test según la TC dependerá de quién lo realice: si los examinados son muy listos, responderán correctamente a las preguntas y, por tanto, el test será considerado fácil. Estas dependencias entre test y examinados supone que las medidas obtenidas en la TC no se pueden utilizar en otros contextos de manera generalizada, y por tanto comparar individuos que hayan hecho exámenes distintos resultará muy difícil (Hambleton, R., 1990).
La Teoría de Respuesta al Item supera esta limitación, pues propone modelos matemáticos orientados a las preguntas (que en este contexto reciben el nombre de ítem), en contraposición a la TC, para el cual la evaluación de conocimientos gira en torno al test como unidad. Se trata de una teoría relativamente joven, data de comienzos de los años 60, habiendo sido implementada por primera vez durante los 80 (López, J., Pérez, T. & Armendáriz, A., 2004).
Dicho de paso, la Psicometría y Edumetría se ocupan de los problemas de medición en Psicología y Educación, utilizando la estadística como pilar básico para la elaboración de teorías y para el desarrollo de métodos y técnicas especificas de medición (Olea, J., Ponsoda, V. , Abad, F., Revuelta, J., Gil, B. & García, C., 2004).
5.1. VISION GENERAL DE AMBAS TEORIAS
En este apartado se analizarán dos de las principales teorías que se utilizan en el ámbito de la medición educacional: La TC y la IRT.
Primero que todo, se hace necesario definir algunos términos. Distintas pruebas miden diferentes características de los examinados, por ejemplo: conocimiento matemático, razonamiento científico, capacidad de memorización, vocabulario, etc. En medición educacional, por “constructo” se entenderá a la característica del examinado que va a ser medida a través de la prueba y, por consiguiente, ésta se utiliza para representar de manera genérica cualquiera de esas características. Por otro lado, en lo que respecta a los ítems de una prueba, hay parámetros (o descriptores) que permiten describir sus atributos particulares. Los parámetros de un ítem que suelen ser más frecuentemente utilizados y, por consiguiente estimados, son:
a) Nivel de Dificultad.
b) Nivel de Discriminación de un Item.
c) Efectos del Azar.
Teoría Clásica
Una forma de medición que se utiliza con mucha frecuencia en pruebas de gran escala, como las de admisión a la universidad (por ejemplo, en el SAT de Estados Unidos y en la PSU en Chile), es la llamada Teoría Clásica. En teoría clásica, el indicador del constructo de un estudiante corresponde al puntaje que se obtuvo en la prueba, construido a partir del número de respuestas correctas (o número de respuestas correctas netas) que obtuvo. Como indicador de la dificultad de una pregunta, en este sistema se utiliza la razón entre el número de personas que acertaron correctamente el ítem y el total de alumnos que dieron una respuesta a éste. Por otro lado, el índice de discriminación de un ítem se calcula como la correlación entre el puntaje de la respuesta a éste y el puntaje en la prueba total. Además en los test formados por ítem de opción múltiple, en las que sólo una alternativa es la correcta, podemos sobrestimar la puntuación directa de una persona dado que alguno de sus aciertos ha podido producirse por azar. El problema entonces consiste en establecer un procedimiento para descontar del número total de aciertos que se han producido por azar. Si se asume que no se conoce la respuesta correcta a un ítem, todas las alternativas de respuesta son equiprobables y la probabilidad de acertar al azar ese ítem se puede establecer como: 1/n, donde n es el número de alternativas del ítem. Estos descriptores de los ítems pueden calcularse ya sea en el contexto de una prueba piloto o experimental, o en la prueba definitiva u operacional.
Como se puede apreciar, en la TC el grado del constructo de una persona depende del grupo de ítems (vale decir, de sus diferentes parámetros) que contiene la prueba. Por ejemplo, si la prueba es fácil, un mismo alumno tendrá un puntaje mayor que si la prueba es difícil. Con esto resulta difícil hacer comparaciones entre estudiantes que han rendido pruebas diferentes. A su vez, la estimación de los parámetros depende del grupo de personas a las cuales se aplicó el test. Así, un mismo ítem puede ser catalogado como fácil si el grupo que rindió la prueba es excepcionalmente hábil, pero como difícil si el grupo que rindió la prueba es desaventajado. Con respecto a la discriminación, un ítem puede aparecer muy discriminativo en el contexto de un grupo con nivel heterogéneo del constructo, pero poco discriminativo si el grupo que rindió la prueba es homogéneo (es decir, si todos los estudiantes tienen un nivel del constructo similar). Esta debilidad, que se genera en la estimación del constructo de los examinados y los parámetros de los ítems, han llevado a buscar un método que permitiese una medida del constructo que sea independiente de los ítems a los que estos se han enfrentado, una caracterización de los ítems independiente de la población a la que se aplica, y al mismo tiempo una medida más fiel de la precisión con que se está midiendo el constructo.
La satisfacción de estos requerimientos se ha intentado encontrar en la Teoría de Respuesta al Item.
Teoría de Respuesta al Item
Los modelos de la IRT se centran en los ítems e intentan establecer, para cada uno de ellos, la probabilidad de ser respondidos correctamente. Esta probabilidad depende del constructo del examinado y de ciertas características de los ítems, entre las que se encuentra el grado de dificultad, discriminación y la probabilidad de ser respondido correctamente por azar por una persona de bajo nivel del constructo. Hay varios modelos en IRT de distinta complejidad. El modelo más simple es aquel que sólo diferencia los ítems según su grado de dificultad. Sin embargo, otros modelos permiten además incluir otros parámetros de los ítems, como su grado de discriminación y la probabilidad de responderlo correctamente al azar.
Aparte de lo anterior, la IRT hace posible conocer el nivel de precisión que un ítem aporta a la estimación para cada nivel del constructo. En términos técnicos esto es lo que se conoce como Información de Fischer, que contextualizado se llama Información del Item. Mientras mayor es la información que aporta el ítem a un determinado nivel del constructo, mayor es la precisión en la estimación de ese nivel.
La principal ventaja teórica de la IRT es que mediante su utilización se lograría que un estudiante obtuviese siempre la misma estimación de su nivel del constructo, independientemente de las preguntas que le tocó responder. También, con la IRT un ítem tendría siempre los mismos parámetros que lo describen (dificultad, discriminación, azar), independientemente del grupo que rindió la prueba. Esta notable propiedad se llama invarianza, siendo ésta la principal ventaja que distingue a la IRT de la Teoría Clásica. Sin embargo, es preciso destacar que la invarianza se cumple siempre y cuando se satisfagan ciertos supuestos y requisitos que se enunciarán a continuación.
Supuestos de la IRT
1. Unidimensionalidad: este supuesto consiste en que en una
prueba todos los ítems están midiendo uno y sólo un constructo en los examinados.
2. Independencia Local: postula que, dado un nivel del constructo, las respuestas
a los ítems no pueden estar correlacionadas entre sí.
3. Igualdad de Educación: que todos los alumnos que rindan la prueba hayan tenido
experiencias educacionales similares.
4. Que la prueba no haya sido apurada, es decir que los tiempos estimados en
el desarrollo de la prueba se respeten.
5. Efectos de Contextos no controlados: se refiere a que algunas preguntas se
comportan de modo diferente según la posición que tenga en la prueba.
Ventajas y desventajas de la IRT
La teoría de respuesta al ítem presenta una serie de potenciales ventajas sobre la teoría clásica. La principal de ellas es la invarianza de los puntajes de la prueba y de las características de las preguntas. También surge, gracias a las curvas de información, herramienta exclusiva de la IRT, la posibilidad de optimizar el proceso de selección de preguntas según el objetivo que se busca.
Todas las ventajas anteriores se pierden cuando los supuestos y requisitos de la IRT no se cumplen. Para que haya invarianza, principal ventaja de la IRT sobre la TC, es fundamental que exista, como se señalaba anteriormente, unidimensionalidad e independencia local. Sin embargo, en muchas ocasiones la naturaleza de las disciplinas mismas les impide someterse a tales restricciones. Es por ello que en la práctica los supuestos y requisitos de la IRT se transgreden (Dussaillant, F. 2003) a menudo. Este incumplimiento de los supuestos lleva no sólo a perder la invarianza sino que afecta directamente a la estimación del constructo e introduce errores en aplicaciones secundarias de la teoría.
6. CONCEPCION DE LA INVESTIGACIÓN
Ya lo señalamos, nuestro trabajo está soportado por marco de la Teoría de las Situaciones Didácticas (Brousseau, 2004), y particularmente en la aproximación antropológica propuesta por Chevallard (1991), caracterizando así tres facetas:
• Saber Sabio generado en las comunidades científicas,
que para esta investigación consideraremos que este saber posee infinitas dimensiones7
no manejables en el sentido estadístico.
• Saber a Enseñar se orienta a la labor del enseñante (i.e., el que enseña)
que debe producir la recontextualización y elección responsable de los conocimientos
que pretenden transformarse en conocimiento para el alumno, es decir, la labor
del enseñante es elegir y construir un modelo (y como tal reduce la complejidad)
adecuado al contexto y al saber sabio, para transformarlo en un saber
adecuado para enseñar.
• Saber Aprendido representa el modelo construido por el alumno como
producto del trabajo intelectual en su interacción con el modelo enseñado.
Como postulado de la investigación se presenta que la calidad del modelo definido por el alumno depende en esencia de la calidad de la transposición didáctica; por otro lado, el saber aprendido se medirá bajo la forma de preguntas y respuestas del tipo Bernoulli (i.e., dicotómicas), orientadas a las dimensiones independientes que constituyen un saber. Asimismo, se asume que los alumnos poseen las competencias básicas para una correcta decodificación.
Pensamos que, a través de este trabajo, podemos iniciar un camino hacia la caracterización de las variables que tienen mayor incidencia en el modelo que el alumno construye en una situación de enseñanza, y en la calidad de éste.
6.1. PROPUESTA
Sean Θ el universo de los saberes sabios, donde cada θ ∈ Θ tiene asociado un conjunto Xθ, constituido por todas las dimensiones de θ, que suponemos es de tamaño no finito, y
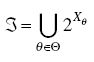
Observemos que 3 es una σ— álgebra sobre {Xθ: θ ∈ Θ}. Por otro lado se define un operador de transposición Γ, cuyo dominio es N una familia de conjuntos finitos de 3, esto es N ⊂ 3, cuyas proyecciones definen, una familia de saberes enseñados, que a través de un proceso de decodificación el alumno lo transforma en saber aprendido.
Esta familia de saberes aprendidos, W, contiene algunas dimensiones y seudodimensiones8 del saber, cuya #W ≤ #N según lo anterior interesa determinar cuáles fueron aquellas dimensiones que constituyen a W que son parte de N además determinar qué tan distante se encuentran estas seudodimensiones de lo que debieran haber sido y, por último, cuál es la distancia existente entre el saber aprendido y saber a enseñar, es decir, cuál es la distancia entre el modelo definido por el alumno a través de la transposición (saber aprendido) y el saber a enseñar.
Adviértase que si #W ≥ # Ψ(Ω), la distancia entre el saber aprendido y el saber a enseñar se considerará nula.
Visualización:
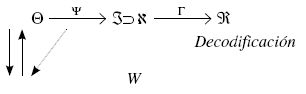
Por otro lado, desde un punto de vista estocástico, consideremos que el poseer la dimensión i-ésima del saber es una variable aleatoria del tipo Bernoulli, donde la probabilidad de éxito está modelada por la siguiente función de distribución,
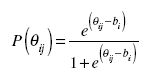
que es función de θij, que represente el nivel de competencia de la j-ésima persona en la i-ésima dimensión del saber θ, además bi represente el nivel de importancia de la i-ésima dimensión del saber en estudio, gráficamente se tiene:
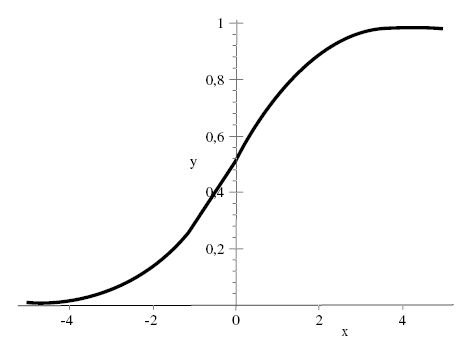
Permitiendo visualizar que a mayor nivel de competencia en la dimensión del saber en estudio (en el gráfico el eje de absisas), mayor es la probabilidad de éxito (eje de ordenadas). Así la probabilidad de que la j-ésima persona construya la i-ésima dimensión está dada por:
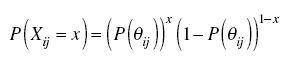
Bajo esta concepción, el problema se reduce a estimar θj, que hace más probable j el constructo definido por el alumno luego del Operador de Transposición, donde el estimador de θj ∈ IR y representa la cuantificación de que tan bueno fue el modelo que j logró definir el alumno respecto del saber, desde esa perspectiva perfectamente se puede definir la distancia euclidiana entre el ideal para θj y su estimación.
7. SIMULACIONES
Sean Xθ un conjunto infinito cuyos elementos son todas las dimensiones de un saber θ ∈ Θ #N = 10, es decir, X posee 10 dimensiones que caracterizan ese saber, sobre este subconjunto de Xθ, denominado N se define un operador de transposición Γ, que transforman esas dimensiones en saber enseñado que el alumno decodificará y transformará en saber aprendido.
Sea T, el test orientado a medir las 10 dimensiones independientes del saber, aplicado a 30 personas.
Basado en la metodología de trabajo que se propone, se tiene:
Distancia
Euclideana de Entre el Saber Aprendido y el Saber a Enseñar |
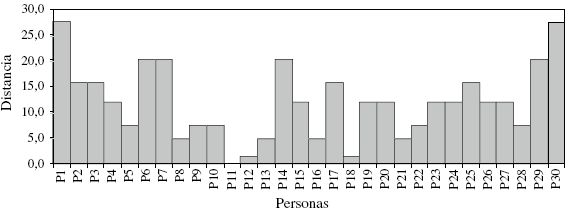 |
Además, podemos especificar respecto del ítem o equivalentemente la dimensión con menor o mayor incidencia en la distancia entre los Saberes, por medio de un estudio correlacional de las puntuaciones a cada ítem y la puntuación total.
Por ejemplo:
Porcentaje
de Incidencias del Item en la Distancia |
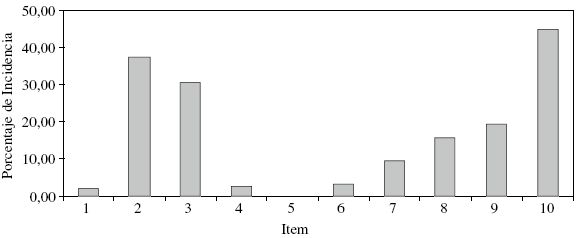 |
En este gráfico podemos hacer mención que los ítems 1, 4, y 5 no alcanzan niveles satisfactorios, permitiendo, de este modo, redefinir la transposición hacia el logro de las dimensiones desfavorecidas o posibilitar otra.
De esta forma podemos reestructurar la definición de los Operadores de Elección y de Transposición en vías de lograr una optimización de estos y, por lo tanto, definir Transposiciones efectivas.
8. CONCLUSIONES
Pensamos que el aporte de este trabajo recae en la dotación de un lenguaje que debiera redundar en la incorporación de nuevas herramientas sin perder el sustento teórico formal que le da la Teoría de Situaciones Didácticas. Este lenguaje se sumerge en la Teoría de Situaciones Didácticas sin provocar colisiones conceptuales, sino que más bien posibilita la incorporación de otras técnicas, particularmente, estadísticas. En este caso, el uso de la IRT respecto de la puesta en obra por parte de los enseñantes permite obtener indicadores más finos y de mayor complejidad, lo que posibilita la toma de decisiones fundadas, iterando hasta que converja al proceso óptimo.
En efecto; se trata de un control del proceso en vías de descubrir debilidades metodológicas, promoviendo los procesos de transposición eficientes para el logro de las dimensiones seleccionadas como características del saber objetivo, además poder determinar la pertinencia e influencia de las dimensiones escogidas como caracterizadores del saber, permitiendo así proponer una metodología de trabajo consistente, evaluable, reformulable, efectiva y comprometida con la educación de calidad.
9. AGRADECIMIENTOS
Paula Sofía Ponce Grenet.
NOTAS
1 Chevallard, Y. (1991). La transposition didactique. Du savoir savant au savoir enseigné, Grenoble, La Pensée Sauvage, Editions (2ième Edition revisada y aumentada, en colaboración con Marie-Alberte Joshua).
2 Le savoir appris par l’élève a, de ce fait, connu trois étapes successives de traduction, de reconstruction. En effet, le «savoir savant» a d’abord subi une transposition didactique à l’issue de laquelle il a été transformé en savoir à enseigner. De ce «savoir à enseigner», l’enseignant en a retenu une version qui constitue le «savoir enseigné». Enfin, l’élève a filtré ces informations pour composer son «savoir appris». (A. Mabille & V. Albert, 1994: p. 14).
3 Equipo Laboratorio [EXPERIMENTAL] de Saberes Matemáticos (i.e., Equipo Lab[e]saM ) inserto en el Departamento de Matemática & Física, Facultad de Ciencias Naturales & Exactas, Universidad de Playa Ancha / Valparaíso, CHILE.
Brousseau, G. (2004). Théorie des Situations Didactiques (Didactiques des Mathématiques 1970-1990). Grenoble: La Pensée Sauvage, Editions (2ième Edition).
4 Chevallard, Y. (1991) La transposition didactique. Du savoir savant au savoir enseigné, Grenoble, La Pensée Sauvage, Editions (2ième Edition revisada y aumentada, en colaboración con Marie-Alberte Joshua).
5 Le savoir appris par l’élève a, de ce fait, connu trois étapes successives de traduction, de reconstruction. En effet, le «savoir savant» a d’abord subi une transposition didactique à l’issue de laquelle il a été transformé en savoir à enseigner. De ce «savoir à enseigner», l’enseignant en a retenu une version qui constitue le «savoir enseigné». Enfin, l’élève a filtré ces informations pour composer son «savoir appris». (A. Mabille & V. Albert, 1994: p. 14).
6 “El trabajo que transforma de un objeto de saber a enseñar en un objeto de enseñanza, es denominado transposición didáctica” [ésta es una traducción libre de los autores de este trabajo].
7 En este trabajo el sustantivo dimensión alude a cada una de las características esenciales del saber.
8 En este caso utilizamos la palabra seudodimensión para hacer alusión a la dimensión de saber que posee el alumno, y que no coincide con las dimensiones del saber enseñado que recibió.
10. BIBLIOGRAFIA
Brousseau, G. (2004). Théorie des Situations Didactiques (Didactiques des Mathématiques 1970-1990). (2a Edición) Grenoble, Francia: La Pensée Sauvage, Editions.
Chevallard, Y. (1991). La transposition didactique. Du savoir savant au savoir enseigné. (2a Edición en colaboración con Marie-Alberte Joshua), Grenoble, Francia: La Pensée Sauvage, Editions.
Cortada de Kohan, N. (2003). Posibilidad de integración de las teorías cognitivas y la psicometría moderna. (pp. 8-23). Argentina: Revista Argentina de Neuropsicología.
Dussaillant, F. (2003). Técnicas de medición en pruebas de admisión a las universidades (p. 98). Santiago, Chile. C.E.P.
Hambleton, R. (1990). Fundamentals of Item Response Theory. (pp. 15-31). Educational Measurement.
López, J., Pérez, T. & Armendáriz, A. (2004). Evaluación Mediante Test, Departamento de Lenguas y Sistemas Informáticos. Universidad del País Vasco, España. Revista Iberoamericana de Educación.
López, J. Pérez, T. & Armendáriz, A. (2004). Evaluación Mediante Test, Departamento de Lenguas y Sistemas Informáticos. Universidad del País Vasco, España. Revista Iberoamericana de Educación.
Mabille, A. & Albert, V. (1994). Profils de profs: Portarait et styles d’enseignants en sciences. (2a Edición) Louvain-la-Neuve, Bélgica: De Boeck Université.
Muñiz, J. (1997). Teoría Clásica de los Test. (pp. 26). Universidad de Oviedo, España. Editorial Pirámide.
Olea, J., Ponsoda, V. , Abad, F., Revuelta, J., Gil, B. & García, C. (2004). Introducción a la Psicometría, Teoría Clásica de los Test y Teoría de la Respuesta al Ítem. Madrid, España: Edición interna de la Universidad Autónoma de Madrid.