* Expresada en meses.
Estudios Pedagógicos XXXVIII, Nº 1: 235-253, 2012
INVESTIGACIONES
Adaptación de la versión española del Test de Evaluación Matemática Temprana de Utrecht en Chile *
An Adaptation of the Spanish version of the Utrecht Early Numeracy Test in Chile.
Adaptação da versão espanhola da Avaliação Temporâ de Matemática de Utrecht, Chile
Gamal Cerda Etchepare 1, Carlos Pérez Wilson 2, Carla Moreno Araya 1, Katherine Núñez Risco 1, Elizabeth Quezada Herrera 1, Jeminal Rebolledo Rojas 1, Soraya Sáez Tisnao 1
1 Facultad
de Educación, Universidad de Concepción, Casilla 160-C, Concepción,
Chile.
2 Facultad de Ciencias Físicas y Matemáticas,
Universidad de Concepción, Casilla 160-C, Concepción, Chile.
* Trabajo parcialmente financiado por el Proyecto I+D Fondef
D06I1069.
RESUMEN
El artículo describe los estudios de validez y confiabilidad llevados a cabo sobre el Test de Evaluación Matemática Temprana Utrech (TEMT-U) que corresponde a una versión española del Utrecht Early Numeracy Test, instrumento que evalúa la competencia general en matemática y las áreas específicas de Comparación, Clasificación, Correspondencia, Seriación, Conteo Verbal, Conteo Estructurado, Conteo Resultante y Conocimiento General de los Números en niños y niñas de edades entre cuatro a ocho años, que cursan desde primer nivel de transición hasta segundo básico (N= 1436, 730 mujeres y 707 varones). Los análisis de validez y confiabilidad realizados sobre este instrumento permiten que el test TEMT-U pueda ser considerado como un instrumento útil para evaluar el desempeño en el área matemática de estudiantes chilenos de Segundo Ciclo Preescolar y Primer Ciclo Básico, en la medida que se reportan puntajes comparativos por edad, nivel educativo y dependencia administrativa.
Palabras clave: matemática temprana, educación preescolar, educación básica, edad, sexo.
ABSTRACT
This work presents the validity and reliability studies conducted on the Spanish version of the Utrecht Early Numeracy Test ("Test de Evaluación Matemática Temprana Utrech", TEMT-U). This instrument assesses the general competence in mathematics and the specific areas of comparison, classification, correspondence, seriation, verbal counting, structured counting, resultant counting, and general knowledge of Numbers. The study was performed in Chilean children aged four to eight years, attending the first level of transition to second grade of elementary school(N = 1436, 730 women and 707 men). The validity and reliability analysis conducted show that TEMT-U test can be considered a useful tool for assessing the mathematical performance of Chilean students of preschool and elementary school. The comparative scores for age, administrative support of school, and gender are presented.
Key words: early mathematics competence, administrative dependence, mathematics, pre-school education, age, sex.
RESUMO
Descrevem-se os estudos realizado sobre validade e confiabilidade da Avaliação Temporâ de Matemática de Utrecht (TEMT-U), a qual corresponde a uma versão em espanhol do Teste de Aritmética Precoce de Utrecht, um instrumento que avalia competências gerais em Matemática e áreas específicas de comparação, classificação, correspondência, seriação, contagem verbal, contagem estruturada, contagem resultante e conhecimentos gerais referentes aos números de conhecimentos gerais resultantes de crianças de quatro a oito anos, que frequentam desde a pré-escola aos oito anos e que cursem o segundo ou terceiro ano do primeiro ciclo da Educação Fundamental (N = 1436, sendo 730 mulheres e 707 homens). Como resultados, afirma-se a Avaliação do TEMT-U como ferramenta útil para avaliar o desempenho de estudantes chilenos da Pré-Escolar e segundo ciclo da primeira etapa da Educação Básica na área de Matemática, na medida em que se considera dados comparativos por idade, nível educacional e unidade organizacional.
Palavra schave: matemática temporâ, educação infantil, educação básica, idade, sexo.
1. INTRODUCCIÓN
En la actualidad en nuestro país existe consenso respecto de la importancia que reviste el aprendizaje y comprensión del conocimiento matemático para la vida de sus ciudadanos. Curiosamente, esta importancia no se condice con el rendimiento insatisfactorio observado en el área, como lo ponen de manifiesto las numerosas mediciones realizadas a nivel nacional e internacional en los niveles de Educación Media y en segundo ciclo Educación Básica, tales como el Sistema Nacional de Evaluación de resultados de aprendizaje del Ministerio de Educación de Chile [SIMCE]; Programme for international Student Assessment [PISA] y Trends in International Mathematics and Science Study [TIMMS] (MINEDUC, 2004; 2006a; 2009).
El diagnóstico de estas investigaciones es lapidario respecto del bajo nivel de logro en matemáticas, especialmente en la educación pública municipalizada, aun cuando la evidencia tampoco es satisfactoria para la educación particular subvencionada y particular pagada, que también muestra desempeños por debajo de las medias internacionales e incluso nacionales para niveles de costo y recursos materiales homologables (Treviño y Donoso, 2010). Las investigaciones también dejan entrever que estos magros resultados permanecen sin cambios importantes y con altos índices de inequidad social en los últimos años.
Sin embargo, estas evaluaciones predominantemente entregan información sobre el rendimiento académico en los niveles educativos contemplados entre finales del primer ciclo básico hasta la Enseñanza Media, no dando cuenta sobre lo que acontece en el nivel inicial, es decir, en los cursos correspondientes a la educación preescolar e inicios del primer ciclo básico.
Esta ausencia de resultados en estos niveles iniciales resulta especialmente preocupante si se considera que es allí donde se gesta la base de los aprendizajes en todas las áreas, gracias al rápido desarrollo cerebral y a las denominadas ventanas de oportunidades, por lo mismo, las experiencias tempranas resultan fundamentales para "la naturaleza, profundización y extensión de las capacidades de la vida adulta" (MINEDUC, 2001:15). De acuerdo al diagnóstico desfavorable en las etapas posteriores de escolarización, cabe preguntarse si es en los niveles iniciales donde surgen o comienzan a manifestarse las deficiencias en el aprendizaje de las Matemáticas. La escasez de estudios de amplia cobertura y la escasez de instrumentos de evaluación de conocimientos matemáticos tempranos hace difícil abordar un estudio de esta naturaleza, en donde, además, las características de la población objetivo dificultan la aplicación de pruebas colectivas autoadministradas de rápida tabulación y análisis. Una excepción a lo anterior lo constituye la Prueba de Precálculo (Milicic & Schmidt, 2008), instrumento creado en Chile el año 1978 para evaluar el desarrollo del razonamiento matemático en niños entre 4 y 7 años de edad.
Por lo anterior, resulta necesario e impostergable, aumentar de forma significativa el número de instrumentos validados en el área de evaluación de las matemáticas a nivel inicial.
Uno de los instrumentos específicamente desarrollados para tales efectos, y que es motivo de numerosos estudios comparativos con otros países, es el Utrecht Early Numeracy Test, creado por Johannes van Luit, Bernadette van de Rijt y Albèr Pennings, en 1994 (Van de Rijt, Van Luit, & Pennings, 1999). Una versión en español de este Test ha sido estandarizada en España (Navarro et al., 2009; 2010) bajo el nombre de Test de Evaluación Matemática Temprana de Utrecht.
El presente trabajo da cuenta del proceso de adaptación de este test, que denominaremos en adelante TEMT-U, para un grupo objetivo de la población escolar chilena, compuesto por niños y niñas de entre 4 y 8 años correspondientes a los niveles de Primer y Segundo nivel de Transición, y Primero y Segundo año básico, de las dependencias administrativas Particular Subvencionada y Municipalizada.
Contar con un instrumento en este ámbito y, además, psicométricamente testeado, podría permitir fundamentar decisiones sobre políticas de intervención, medidas remediales o cursos de acción preventivos que promuevan mejores logros de aprendizaje futuro en matemáticas. Por cierto, un diagnóstico en esta edad debe tener un carácter eminentemente formativo y orientador, en la medida en que permite identificar las principales áreas de dificultad o habilidades poco desarrolladas, como también aquellas habilidades sólidamente consolidadas o en proceso de consecución. De esta manera, se proporciona información pertinente a los agentes y educadores, quienes podrán planificar intervenciones educativas, innovaciones y evaluaciones seguimiento o de progreso.
1.1. COMPETENCIAS MATEMÁTICAS TEMPRANAS
El concepto de competencia en el área de las matemáticas implica, de acuerdo a Niss (1999), la habilidad de entender, juzgar, hacer y usar las matemáticas en una variedad de situaciones y contextos intra y extra matemáticos, en los que éstas juegan o podrían jugar un rol. Estas habilidades pueden hacerse manifiestas en diversos niveles de complejidad, pues dependen de los sujetos que las poseen y del modo en que éstas son movilizadas como respuesta a las demandas del entorno y situaciones específicas (Rico y Lupiánez, 2008). A nivel inicial, según Cardoso y Cereceda (2008), la competencia matemática se hace explícita con las demandas y entorno propio de dicha edad, pues exige que el niño o la niña realice una manipulación de los objetos matemáticos, desarrolle su creatividad, reflexione sobre su propio proceso de pensamiento a fin de mejorarlo, se divierta con su propia actividad mental, haga transferencia a otros problemas de la ciencia y de su vida cotidiana, adquiera confianza en sí mismo y se prepare paulatinamente a los nuevos retos de la tecnología.
Numerosas investigaciones permiten vislumbrar cómo se desarrollan estas habilidades matemáticas a temprana edad. Baroody (2002) y Bryant y Nunes (2002), entre otros, ponen de manifiesto que un niño es capaz de diferenciar tempranamente dónde hay más elementos y dónde hay menos, sin poder aún cuantificar cuántos elementos existen en cada conjunto. Se ha encontrado que alrededor de los 2 años surgen los primeros intentos de usar los números convencionales en situaciones concretas (Bermejo, 1994). Starkey y Cooper (1980) encontraron que bebés de 5 meses discriminaban entre 2 y 3 puntos.
Wynn, Bloom y Chiang (2002) encontraron evidencias de que niños y niñas de 5 meses podían individualizar y contar colecciones de objeto, cuestión que confirma los antecedentes reportados previamente por los estudios de Uller et al. (1999), Baillargeon (1994) y Sarnecka y Carey (2008). Del mismo modo, Brannon (2002), encontró evidencia que la comprensión de las relaciones ordinales se produce entre los 9 a los 11 meses de edad, incluso antes que los niños y niñas sean capaces de emitir la secuencia de conteo. Estas y otras múltiples investigaciones permiten afirmar que los niños y niñas a corta edad conocen los aspectos relacionados con la cardinalidad del número, reconociendo si dos conjuntos son o no del mismo tamaño. Más aún, algunas investigaciones en el ámbito de las neurociencias han planteado el fuerte sustrato neuronal de la noción de número en niños muy pequeños, como lo es el lóbulo parietal del cerebro (Chen y Walsh, 2009).
El desarrollo teórico y los estudios en el área, paulatinamente fueron decantando en ciertas líneas teóricas que dieron origen al enfoque interaccionista que propone Van de Rijt (1996) y Van de Rijt y Van Luit (1998), que forman la base de la denominada competencia matemática temprana. Este enfoque integra los aspectos del pensamiento lógico u operaciones piagetianas y las experiencias de conteo como contribución inequívoca al desarrollo del número.
El pensamiento lógico, la enseñanza de la numeración convencional y el aprendizaje significativo y contextualizado de los contenidos matemáticos serían, a juicio de Bryant y Nunes (2002), la base del desarrollo matemático. Esta perspectiva se enmarca dentro del denominado enfoque piagetiano (Baroody, 1998; Dehaene, 1997). De acuerdo a los estudios y observaciones de Piaget, los niños desarrollan lo que él denomina "matemática intuitiva"; pues son capaces de señalar cuándo se le presenta una suma o resta por medio de objetos, agregando o quitando elementos de un recipiente, pero no son capaces de diferenciar, con igual claridad, situaciones cuando se agregan más o distinto número de elementos simultáneamente en dos fuentes; observándose, por ejemplo, que los niños afirman que la fuente que tiene más objetos es a la que se le agregaron y no la que contiene mayor cantidad. Según esta perspectiva, hasta que los niños no alcanzan la etapa de las operaciones concretas, no es posible hablar de una comprensión real del número (Piaget, 1959). Además, para Piaget (1965) existen requisitos lógicos que son determinantes para comprender el número, los que están interrelacionados entre sí, y sólo al ser alcanzados los requisitos básicos se desarrolla la comprensión.
Por otra parte, Gelman y Gallistel (1978), Gallistel (1978), Barouillet y Camos (2002) y Lehalle (2002) sostienen que las competencias matemáticas se desarrollan gradualmente a través de la ejercitación de actividades de conteo, las cuales contribuyen a desarrollar destrezas matemáticas y que, posteriormente, permiten que el menor pueda automatizarlas y usarlas eficazmente.
El constructo competencia matemática temprana presupone que las denominadas operaciones lógicas piagetianas y las habilidades de conteo contribuyen de forma significativa al desarrollo matemático, aun cuando algunos estudios dejan entrever que la aportación de esta última habilidad es mayor que la atribuida a las operaciones lógicas (Nunes y Bryant, 1996). Un aporte señero en el área fue el estudio de Clements (1984), que mostró que niños de cuatro años sometidos a un programa de entrenamiento en destrezas de conteo mejoraba de forma significativa en las habilidades involucradas en seriación y clasificación. Aun cuando estas habilidades son interdependientes, el entrenamiento en conteo es preferible porque produce un efecto mayor que el entrenamiento en seriación y clasificación. En esta misma dirección, las investigaciones de Cowan, Foster y Al-Zubaidi (1993) y de Resnick (1989) dan cuenta de los esquemas protocuantitativos, como precursores del desarrollo matemático posterior, y las de Aunio, Hautamäki y Van Luit (2005), respecto al impacto positivo de programas para reforzar este sentido del número en preescolares con bajos niveles de logro, fortalecen la relevancia de esta capacidad.
La teoría interaccionista propone ocho componentes básicos, los cuales establecen la base de las matemáticas tempranas, las que a su vez se homologan a la estructura de la escala de evaluación matemática temprana. La adquisición de dichas competencias matemáticas básicas es un requisito para ser capaz de seguir una educación matemática formal (Van de Rijt, Van Luit y Pennings, 1999), puesto que permiten continuar en la adquisición de conocimientos y habilidades matemáticas más complejas en las etapas posteriores.
Por lo tanto, si un niño o niña en edad preescolar posee un buen nivel de competencia matemática, es posible esperar resultados satisfactorios en etapas posteriores de su escolaridad. Un estudio realizado por Jordan, Kaplan, Locuniak y Raminemi (2007), donde se examinó el nivel de competencias matemáticas en niños y niñas de nivel preescolar en función de su edad de ingreso al jardín infantil, su género, y nivel de ingresos familiar, puso de manifiesto que el nivel observado en esta variable es un fuerte predictor de los logros matemáticos al final del primer grado. Asimismo, Jordan, Mulhern y Wylie (2009) sostienen que un nivel alto de competencia matemática en el jardín infantil predice de forma significativa los logros matemáticos posteriores, incluso hasta 3º año de primaria. Los estudios de Locuniak y Jordan (2008) y Mazzocco y Thompson (2005) agregan que las primeras competencias matemáticas predicen los resultados a futuro, incluso por sobre las competencias cognitivas, verbales, espaciales y habilidades de memoria del sujeto. En la misma perspectiva, los estudios longitudinales de Byrnes y Wasik (2009), Clarke y Shinn (2004), Krajewski y Scheneider (2009), Lembke y Foegen (2009) y Methe, Hintze y Floyd (2008) indican que las habilidades de conteo, discriminación de cantidades, reconocimiento de números, así como del cálculo verbal y no verbal, son fuertes predictores de logros en matemática a futuro y estarían relacionadas con el nivel y ritmo de aprendizaje de las matemáticas durante los primeros niveles de escolaridad (Locuniak y Jordan, 2008). Esto es congruente con estudios que han examinado cómo la presencia de procesos cognitivos superiores a temprana edad, tales como la conciencia fonológica y la espacial y los mecanismos de control ejecutivo, pueden predecir o bien explicar el desempeño diferenciado en matemáticas (Geary et al., 2009; Stock, Desoete y Roeyers, 2009; Swanson, 2006).
Por otra parte, aun cuando se constata que las competencias matemáticas evidencian una gran variabilidad individual entre preescolares (Van de Rijt y Van Luit, 1998), los estudios longitudinales muestran que dichas diferencias se mantienen a lo largo del desarrollo, y que los estudiantes tienden a permanecer en el mismo rango con respecto a sus iguales a lo largo de la escolaridad primaria y secundaria. Incluso puede llegar a darse que las diferencias tempranas se incrementan conforme se avanza a lo largo de los años de escolaridad (Aubrey, 1993).
Estos hallazgos sugieren que reforzar el aprendizaje matemático en la escolaridad temprana podría reportar un gran beneficio para los estudiantes a lo largo del tiempo, relevando con ello la posibilidad de contar con instrumentos válidos y estandarizados, que evalúen el nivel que presentan las competencias matemáticas tempranas en los niveles iniciales de estudiantes chilenos.
Por todo lo anterior es que los autores del presente estudio han realizado el proceso de adaptación del Test de Evaluación Matemática Temprana de Utrecht (TEMT-U) en la población escolar de niños y niñas de entre 4 y 8 años, de los niveles de Primero y Segundo nivel de Transición, y Primero y Segundo año Básico, en instituciones escolares de dependencia administrativa Particular Subvencionada y Municipal. Este trabajo reporta, además los principales hallazgos asociados al evaluar dichas competencias en la población escolar antes indicada.
2. METODOLOGÍA
La presente investigación se enmarca en un enfoque cuantitativo de tipo descriptivo correlacional, ya que postula caracterizar y dar cuenta de los niveles y rasgos distintivos de las áreas de competencia matemática en un grupo representativo de la población preescolar y de enseñanza básica, y los factores asociados a dicho desempeño.
2.1. INSTRUMENTO
El TEMT-U, versión española del Utrecht Early Numeracy Test, creado por Johannes van Luit, Bernadette van de Rijt y Albèr Pennings, en 1994 (Van de Rijt, Van Luit, & Pennings, 1999), examina dos dimensiones principales de la competencia matemática temprana, los propiamente piagetianos o subtest relacionales y el subtest numérico. El test dispone de tres formas paralelas (denominadas versiones A, B y C), de 40 ítems cada una. En la presente investigación se trabajó con la forma A, que consta, al igual que las otras, de 8 áreas de competencia, en grupos de 5 ítems cada una. El Test tiene una puntuación máxima de 40 puntos, uno por cada ítem correcto. Las dimensiones, siguiendo la descripción de la versión española del test (Navarro et al., 2009), corresponden a los siguientes (la descripción de los componentes transcribe la descripción de la versión española del TETM realizada por el equipo de investigadores de la Universidad de Cádiz, dirigido por José Navarro, 2009):
1. Conceptos de comparación. Este aspecto se refiere al uso de conceptos de comparación entre dos situaciones no equivalentes relacionados con el cardinal, el ordinal y la medida. Son conceptos usados con frecuencia en las matemáticas: el más grande, el más pequeño, el que tiene más, el que tiene menos, etc.
2. Clasificación. Se refiere al agrupamiento de objetos basándose en una o más características. Con la tarea de clasificación se pretende conocer si los niños y niñas, basándose en la semejanza y en las diferencias, pueden distinguir entre objetos y grupos de ellos.
3. Correspondencia uno a uno. Este subtest evalúa el principio de correspondencia uno a uno (también denominada correspondencia término a término). Los niños y niñas deben ser capaces de establecer esta correspondencia entre diferentes objetos que son presentados simultáneamente.
4. Seriación. La seriación consiste en ordenar una serie de objetos discretos según un rango determinado. Se trata de averiguar si los niños son capaces de reconocer una serie de objetos ordenados. Los términos usados en esta tarea son: ordenar de mayor a menor, del más delgado al más grueso, de la más pequeña a la más grande.
5. Conteo verbal (uso de la secuencia numérica oral). En este subtest se evalúa la secuencia numérica oral hasta el 20. La secuencia puede ser expresada contando hacia delante, hacia atrás y relacionándola con el aspecto cardinal y ordinal del número.
6. Conteo estructurado. Este aspecto se refiere a contar un conjunto de objetos que son presentados con una disposición ordenada o desordenada. Los niños y niñas pueden señalar con el dedo los objetos que cuentan. Se trata de averiguar si son capaces de mostrar coordinación entre contar y señalar.
7. Conteo resultante o resultado del conteo (sin señalar). El niño o la niña tienen que contar cantidades que le son presentadas como colecciones estructuradas o no estructuradas y no se le permite señalar o apuntar con los dedos los objetos que tiene que contar.
8. Conocimiento general de los números. Se refiere a la aplicación de la numeración a las situaciones de la vida diaria que son presentadas en formas de dibujo.
2.2. PROCEDIMIENTO:
Por las características de aplicación individual del TEMT-U, fue necesario desarrollar un periodo de familiarización, especialmente con los niños y niñas de nivel preescolar de la muestra. Una vez que los niños y niñas tuvieron confianza con las educadoras a cargo de la aplicación, se procedió a la evaluación uno a uno en una zona tranquila de cada jardín o colegio durante aproximadamente 20 a 30 minutos. Todas las evaluaciones fueron hechas con el consentimiento informado por parte de los padres y autoridades de las instituciones. En la hoja de respuesta se consignaron a los datos personales, otros campos de interés, como la fecha de administración del test y la fecha de nacimiento del niño, permitiendo establecer la edad en meses.
Se comenzaba la prueba diciendo, por ejemplo: "Vamos a jugar un rato a las matemáticas. Va a ser muy fácil. Trata de hacerlo lo mejor que sepas". Si el niño no comprendía las preguntas, se permitía repetir las instrucciones otra vez. De vez en cuando se recompensaba el esfuerzo del niño por el esfuerzo que realizaba, diciéndole frases como "lo estás haciendo muy bien" o "buen trabajo".
Se debe señalar que, previamente, se habían realizado aplicaciones piloto de este instrumento a grupos de niños de diversas edades para verificar que las instrucciones y tareas eran comprendidas correctamente. En cuanto a las posibles modificaciones en los enunciados producto de las variaciones o giros lingüísticos, no hubo ningún cambio significativo respecto de la versión original, cuestión que fue avalada por jueces expertos, educadoras en ejercicio y profesores universitarios de la carreras de la infancia.
2.3. POBLACIÓN Y MUESTRA
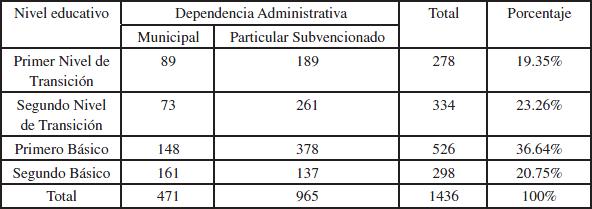
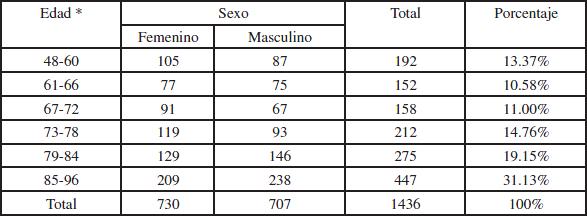
Se procedió a estratificar la población escolar por tipo de establecimientos: Municipales y Particulares Subvencionados. La estratificación consideró además la edad, el nivel académico o curso y el sexo de los sujetos. La unidad muestral quedó constituida por estudiantes, niños y niñas, cuyas edades fluctúan entre los cuatro y ocho años, que asisten a Primer y Segundo Nivel de Transición del nivel Preescolar, y de Primero y Segundo año Básico del Primer ciclo básico, pertenecientes a establecimientos de dependencia Municipal y Particular Subvencionada, de las comunas de Concepción, Hualpén, Talcahuano, San Pedro de la Paz y Villarrica.
La muestra final de estudiantes, seleccionados de manera aleatoria, estuvo compuesta por un total de 1437 niños y niñas pertenecientes a 16 instituciones educativas de dependencia Municipal y Particular Subvencionada. La proporción según sexo es equilibrada con un 50.8% femenino y un 49.2% de participantes masculinos.
Las Tablas 1 y 2 presentan la distribución de la muestra final de estudiantes por categorías de estudio.
 * Expresada en meses. |
 |
2.4. ANÁLISIS ESTADÍSTICOS
Los análisis estadísticos que a continuación se presentan, buscan respaldar el ajuste del TEMT-U a los índices y medidas requeridas para los procesos de adaptación y validación de acuerdo a los estándares de la comunidad científica. Por ello, se ha determinado los índices de dificultad de sus ítems constitutivos, se ha determinado su confiabilidad a través del cálculo del coeficiente alpha de Cronbach y se ha estudiado su validez mediante el análisis factorial exploratorio. También, se aplicaron análisis de estadística descriptiva e inferencial, como medias, desviaciones típicas, prueba t, correlaciones producto Momento de Pearson y ANOVA. Para el análisis de los resultados se utilizó el programa SPSS® versión 15.
3 RESULTADOS
3.1. ANÁLISIS DE LOS ÍTEMS
De acuerdo a la clasificación de García, Pérez y Del Río (1999), hay un 52,5% de ítems Muy Fáciles (I.D. por encima de 0,75); un 30% de ítems Fáciles (I.D. entre 0,55 y 0,74); un 10% de ítems Normales (I.D. entre 0,45 y 0,54); un 7,5% de ítems Difíciles (I.D. entre 0,25 y 0,44). No se observan ítems en la categoría Muy Difíciles, (I.D. por debajo de 0,25).
3.2. ANÁLISIS DE LA FIABILIDAD Y VALIDEZ DEL TEMT-U
La confiabilidad del test TEMT-U fue calculada a partir del coeficiente Alfa de Cronbach, el cual mide la consistencia interna del instrumento evaluativo. Se obtuvo un índice rα=0,915, lo cual establece que el instrumento es confiable, pudiendo por tanto inferir que la variabilidad de los puntajes observada en el desempeño de los niños y niñas responde a la variabilidad esperada en la característica evaluada y no es fruto del azar. Al calcular la fiabilidad de la dimensión relacional se obtuvo un índice rα=0,71 y para la dimensión numéricos se obtuvo un índice rα=0,897, ambos valores aceptables desde el punto de vista psicométrico.
3.3. ANÁLISIS DE VALIDEZ
Para comprobar la unidimensionalidad de los resultados del test se calculó la matriz de correlaciones entre los puntajes respectivos de cada uno de los ocho subtests y el total de la puntuación alcanzada. Se observó que las ocho áreas de competencia están fuertemente correlacionadas entre sí, lo que permite inferir que éstas están vinculadas a una misma competencia matemática subyacente, lo que es corroborado por los índices de correlación positivos y significativos al 99% de confianza entre los puntajes de los subtest y la puntuación total.
Esta inferencia se ve corroborada al llevar a cabo un análisis factorial exploratorio de la matriz de correlaciones. Para determinar el número de factores presentes en el conjunto de variables se empleó como criterio el análisis paralelo de Horn combinado con un remuestreo basado en 5000 muestras obtenidas mediante bootstraping a partir de las variables originales. El resultado obtenido mostró que sólo el primer valor propio de la matriz de correlaciones de las variables analizadas (tres primeros valores propios: 4,62, 0,81 y 0,69) logró superar al cuantil 95 de los valores propios correspondientes obtenidos a partir de las remuestras bootstraping (tres primeros valores propios: 1,15, 1,10 y 1,06). Este resultado lleva a concluir la existencia de un solo factor para el conjunto de variables.
En virtud de los resultados recién descritos, se procedió a solicitar la extracción de un solo factor mediante un Análisis de Eje Principal. En cuanto a la varianza explicada por la solución de un factor esta correspondió al 52,46%. La Tabla 3 presenta la matriz de cargas factoriales para dicha solución factorial.
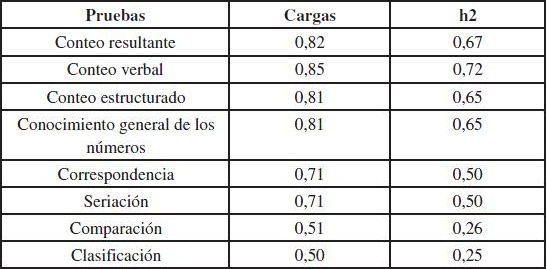 |
3.4. NIVELES DE COMPETENCIA MATEMÁTICA TEMPRANA Y FACTORES ASOCIADOS
A nivel general, el desempeño de la muestra total en el TEMT-U presenta un rendimiento promedio de 29,75 puntos, con una desviación típica de 7,83 puntos. Recordemos que el puntaje ideal de la prueba es de 40 puntos. Se observa que los resultados en el Subtest Relacional son superiores que en el Subtest Numérico (M= 16,35, DT= 3,11 y M= 13,46, DT= 5,16 respectivamente).
Al analizar los desempeños de la muestra en función del nivel educativo, éstos presentan un aumento progresivo y consistente, como se observa en los histogramas de frecuencias comparativas de puntajes obtenidos por los niños y niñas en cada uno de los subtest (Figura 1 Subtest Relacionales y Figura 2, subtest Numéricos).
Figura 1. Histograma
comparativo de distribución de frecuencias de puntajes totales
en el TEMT-U por nivel educativo en el subtest Relacional. |
Figura 2. Histograma
comparativo de distribución de frecuencias de puntajes totales
en el TEMT-U por nivel educativo en el subtest Numérico.por
nivel educativo en el subtest Relacional. |
Al analizar los resultados en cada una de las ocho competencias matemáticas, se observa que las tareas de conteo resultante y conteo estructurado resultan ser los más difíciles para los niños y niñas de la muestra y, a la vez, son los que presentan un mayor nivel de heterogeneidad. La Tabla 4 resume las medias aritméticas y desviaciones típicas en cada uno de los ocho subtest, sobre la base de un puntaje máximo de 5 puntos.
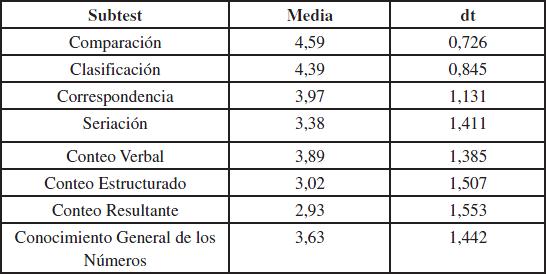 |
Los resultados anteriores presentan el desempeño a nivel de la muestra total. Si se desagregan estos resultados por grupos de edad, se obtiene la información que resume la Tabla 5, la cual permite visualizar las puntuaciones medias alcanzadas en el subtest relacionales y en el subtest numéricos, como también en la puntuación global.
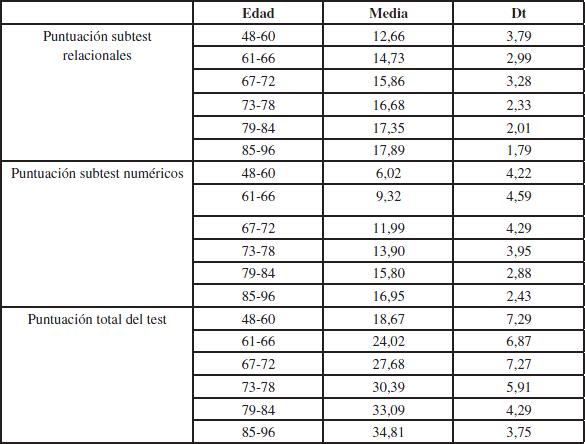 |
4. DISCUSIÓN DE LOS RESULTADOS
Al igual que en otros países que han realizado adaptaciones y validaciones del Utrecht Early Numeracy Test, tales como Holanda, Finlandia, Alemania y España (Aunio et al., 2006; Navarro et al., 2009; 2010; Van de Rijt, Van Luit y Pennings, 1999), el instrumento reúne las características psicométricas adecuadas para evaluar las competencias matemáticas de niños y niñas de 4 a 8 años en la población escolar chilena. Lo anterior permite alcanzar favorablemente al propósito fundamental de la investigación, referida a que el TEMT-U cuenta con niveles de validez y consistencia interna adecuados para ser aplicado a los alumnos de 1er y 2º Nivel de Transición de Educación Parvularia y 1er y 2º año Básico de establecimientos Municipalizados y Particulares Subvencionados de nuestro país. Más aún, los índices reportados en el análisis factorial son muy similares a los resultados publicados en el estudio original de Utrecht Early Numeracy Test, en donde el resultado del análisis factorial exploratorio también mostró un solo factor, con un valor de 4,80, que explicaba el 60% del total de la varianza (Van de Rijt, Van de Luit y Pennings, 1999); en el estudio español, el factor explica el 69% de la varianza (Navarro et al., 2009); recordemos al efecto que, en nuestro estudio, el factor alcanza un valor de 4,62 y explica el 57,8% del total de la varianza. Lo anterior indica que el TEMT-U evalúa destrezas matemáticas diferentes pero con una relación interna, una aptitud o competencia matemática general, que daría cuenta de una capacidad destacada de la interacción de dichas aptitudes específicas. Se podría inferir que la especificidad de las distintas capacidades asumiría la variabilidad restante. Del mismo modo, el índice de confiabilidad del instrumento en su conjunto como los subtest relacionales y subtest numéricos, permiten respaldar que, al evaluar la competencia matemática de los niños y niñas de esta edad y nivel educativo, los resultados observados se pueden adjudicar a las variabilidades propias de su competencia más que al azar y, por lo tanto, podemos presumir que enfrentados a dicho examen en una segunda instancia sus resultados deberían ser similares.
El análisis realizado sugiere que los niños y niñas que rinden el TEMT-U, desde temprana edad, tienen mayor probabilidad de resolver correctamente las tareas del subtest relacional, especialmente aquellos ítems de comparación, seguida de aquellas tareas de clasificación, correspondencia y seriación. Las puntuaciones más bajas encontradas en las cuatro dimensiones del subtest numérico o cognitivo concuerdan con el fundamento de carácter evolutivo del TEMT-U, sobre todo por el hecho de que aunque puedan haber ciertas habilidades de conteo que surjan tempranamente, como lo señalan los estudios de Gelman y Gallistel (1978), otras se desarrollan con posterioridad, como las tareas relacionadas al conteo verbal y conteo estructurado, que son precisamente las que presentan los puntajes medios más bajos. Al cotejar estos resultados con aquellos obtenidos por Van de Rijt y Van de Luit (1999) en grupos de edad comparable, se observan similitudes: las medias obtenidas en ambos subtest son similares, principalmente en el de las competencias relacionales o piagetianas. También se observa el patrón de promedios más altos en este tipo de competencias por sobre los promedios alcanzados en las denominadas competencias numéricas de forma similar a los reportados en Finlandia, Inglaterra, Singapur, Hong Kong y China (Aunio et al., 2004; Aunio et al., 2006; Ee, Wong y Aunio, 2006); también se encontraron diferencias a favor de las competencias relacionales por sobre las numéricas en España (Alcalde et al., 2006; Navarro et al., 2009; 2010).
Por lo tanto, si los procesos educativos en la temprana infancia pueden orientarse a propiciar actividades y aprendizajes tendientes a fortalecer habilidades como completar una secuencia, discriminar cantidades, diferenciar e identificar números u otros, podrían atenuarse de forma significativa las probabilidades de fracaso en el área de matemáticas y el logro de su comprensión (Clarke & Shinn, 2004, Geary et al. 2009; Jordan et al., 2009; Stock, Desoete y Roeyers, 2009; Swanson, 2006).
En las habilidades referidas al subtest Numérico, los alumnos y alumnas de menor edad, esto es, aquellos pertenecientes al Primer y Segundo Nivel de Transición, alcanzan puntajes medios considerablemente más bajos, lo que se debe a que la mayoría de las habilidades contempladas en las tareas de conteo exigen el uso de la abstracción, que es una capacidad mental de nivel superior que comienza a desarrollarse hacia los seis años de edad. Esto concuerda con los períodos que postula Piaget al establecer que un niño o niña, al llegar a los 6 años de edad, es capaz de utilizar la abstracción y resolver problemas en forma mental y con lógica, al finalizar el periodo preoperacional (Woolfolk, 2006). No ocurre lo mismo en los resultados de medias del subtest Relacional, ya que en las áreas que evalúa este subtest, los niños y niñas pequeños ya poseen nociones y son capaces de responder en forma acertada la mayoría de las tareas, como ocurre en la tarea de Comparación y Clasificación, en la que alcanzan las medias más altas, seguidas por las tareas de Seriación y Correspondencia. Sin embargo, y en función de los antecedentes teóricos del enfoque interaccionista, esto podría tener su explicación en el diseño del currículo de la Educación Parvularia, currículo en el cual, a través de los Programas Pedagógicos para el Nivel de Transición 1 y Nivel de Transición 2, en el núcleo de Relaciones Lógico-Matemáticas y de Cuantificación, el énfasis es puesto en el logro de aprendizajes esperados relacionados con el desarrollo de competencias matemáticas, los cuales en su mayoría están orientadas a potenciar de forma progresiva habilidades tales como Comparación, Clasificación, Seriación y Correspondencia y, en menor medida, los relacionados con las habilidades de cuantificación (MINEDUC, 2008). De esta forma, las Educadoras de Párvulos, parecen planificar las experiencias de aprendizaje diarias en el área enfocándose en estimular con mayor énfasis y consistencia estas habilidades desde la temprana infancia. Sin embargo, aceptar esta explicación del porqué los resultados en los niños y niñas de Preescolar, se ven beneficiados en el subtest Relacional por sobre el subtest Numérico del TEMT-U, requiere mayor investigación al respecto.
El estudio de las diferencias por sexo indicó que no existen diferencias significativas en los niveles de Competencia Matemática Temprana entre niños y niñas, ratificando los hallazgos del estudio original de Van de Rijt, Van Luit y Pennings (1999). Estas diferencias respecto del género son independientes del nivel educativo o dependencia administrativa. Si bien en el estudio el sexo masculino alcanza puntajes medios levemente más elevados que el sexo femenino, el análisis estadístico refleja que estas diferencias no son significativas. Estos resultados reafirman lo evidenciado en otras investigaciones, donde se descubrió que las diferencias de género en el rendimiento de las Matemáticas en los primeros años no son significativas (Klein, Adi-Japha y Hakak-Benizri, 2010; Navarro et al., 2009, 2010; Van de Rijt, 1996) y que, además, presentan un patrón evolutivo según el cual los niños superan a las niñas al llegar a la adolescencia, siendo su rendimiento significativamente más alto (Hyde, Fennema y Lanon, 1990; Willms y Jacobsen, 1990). El análisis de los datos entregados por la evaluación SIMCE del año 2006, aplicada a los alumnos de 4º Básico y 2º año Medio, confirma la tendencia anteriormente expuesta, ya que se detectó que para el caso de los alumnos de cuarto básico, las diferencias de puntaje en Matemáticas entre hombres y mujeres no son significativas, 249 y 245 puntos respectivamente. Sin embargo, al comparar los resultados obtenidos por hombres y mujeres de 2º año Medio, la diferencia se hace más notoria puesto que el sexo masculino aumenta considerablemente su puntaje en el área, alcanzando los 257 puntos, mientras las mujeres sólo alcanzan 247 puntos (MINEDUC, 2007b; 2007c).
Es interesante hacer ver que existen investigaciones de otros países que muestran que estas diferencias sí pueden ser significativas, como lo es el caso de Finlandia. En dicho país, los resultados indican la existencia de diferencias significativas a favor del sexo femenino, las que alcanzaron medias más altas que los varones (Aunio et al., 2006).
5. COMENTARIOS FINALES, PROYECCIONES Y SUGERENCIAS
En la actualidad, la educación preescolar chilena cuenta con escasos instrumentos evaluativos en el área de las Matemáticas, muchos de los cuales han sido estandarizados hace más de diez años. Lo anterior dificulta la labor de los profesionales de la educación al no poder contar con herramientas adecuadas para la detección de los conocimientos y competencias de sus alumnos en esta área. Tales competencias son fundamentales para que el individuo adquiera conocimientos matemáticos de orden superior a lo largo de la vida. La OCDE define de la Competencia Matemática como "la capacidad de un individuo para identificar y entender el rol que juegan las Matemáticas en el mundo, emitir juicios bien fundamentados y utilizar las matemáticas en formas que le permitan satisfacer sus necesidades como ciudadano constructivo, comprometido y reflexivo" (Rico, 2007: 49).
La integración del test TEMT-U al sistema educativo permitiría someter a prueba los distintos programas de intervención matemática existentes en el país al permitir realizar estudios comparativos entre grupos control y experimental.
Esta herramienta evaluativa adaptada y validada en el contexto educativo nacional se constituye en un aporte a la batería de test existentes en Chile para el área Matemática en el sector preescolar, con la ventaja adicional de ser un instrumento utilizado actualmente por educadores de países como Holanda, España, Singapur y Finlandia. Este hecho podría permitir en futuras investigaciones, con adecuados estudios estadísticos, realizar ciertas comparaciones entre los niños de los diferentes países.
Junto a las características de validez y confiabilidad aquí presentadas, el TEMT-U posee practicidad, ya que es un test con un protocolo de inducción y aplicación adecuado, que contempla instrucciones con un nivel de comprensión adecuado para los niños y niñas. Su hoja de respuestas permite registrar la performance en cada una de las 40 tareas, y a su vez, facilita sintetizar los puntajes en cada una de las ocho dimensiones y los respectivos subtests relacionales y numéricos. El manual y sus instrucciones permiten cautelar la objetividad de corrección y la uniformidad de las instrucciones orales que sirven de encabezado o premisa de las tareas. Por su naturaleza de aplicación individual es necesario establecer un rapport o ambiente adecuado de confianza con el niño o la niña, como también, contar con un espacio físico cómodo, con adecuada iluminación y sin ruidos que entorpezcan su desarrollo.
Su aplicación permite al docente o especialista contar con una visión fundamentada de las fortalezas y debilidades del aprendizaje de la matemática a temprana edad. Este diagnóstico le permite estructurar o aplicar actividades de refuerzo en las áreas deficitarias detectadas, como también la consolidación y mantenimiento de aquellos aspectos destacados o normales para su edad.
Conjuntamente con la tabulación del puntaje alcanzado en cada subtest, dimensión o tarea específica, el especialista o administrador puede observar las estrategias utilizadas por los niños y niñas durante la resolución de los problemas. Este proceso puede entregar información relevante respecto de la recurrencia, modalidad o adecuación de las estrategias, algoritmos emergentes o secuencia de pasos que ponen en escena los niños y niñas de esta edad al resolver problemas. Un problema o tarea específica puede mostrar que un niño o niña responde rápidamente o toma un tiempo para dar la respuesta, puede contar mentalmente sin referir a los objetos o bien puede contar indicando o apoyándose en los mismos, en una especie de numeración punto a punto. Estas observaciones permiten complementar la evaluación de competencia matemática entregada por el TEMT-U al reportar evidencias sobre el nivel avanzado o básico de las estrategias involucradas, especialmente en el denominado subtest numérico o cognitivo.
Un estudio interesante de realizar sería aquél de complementar los antecedentes de adecuación y pertinencia del TEMT-U a través de un estudio de validación concurrente con la prueba de Precálculo de Milicic y Smith, pues poseen dimensiones o componentes similares.
REFERENCIAS BIBLIOGRÁFICAS
Alcalde, C., Aguilar, M. Marchena, E. Y Ruiz, G. (2006). Desarrollo de las capacidades relacionales y de conteo evaluadas por el test de Utrech. International Symposium on Early Mathematics, Actas, 209–227.
Aubrey, C. (1993). An investigation of the mathematical knowledge and competencies which children bring into school. British Educational Research Journal, vol. 19, n.1, 27-41.
Aunio, P., Ee, J., Lim, A., Hautamäki, J. Y Van Luit, J. (2004). Young children's number sense in Finland, Hong Kong and Singapore. International Journal of Early Years Education, vol.12, n.3, 195-216.
Aunio, P., Hautamäki, J. y Van Luit, J. (2005). Mathematical thinking intervention programmes for preschool children with normal and low number sense. European Journal of Special Needs Education, vol. 20, n.2, 131-146.
Aunio, P., Hautamäki, J., Sajaniemi, N. y Van Luit, J. (2009). Early numeracy in low-performing young children. British Educational Research Journal, vol.35, n.1, 25-46.
Aunio, P., Niemivirta, M., Hautamäki, J., Van Luit, J., Shi, J., y Zhang, M. (2006). Young children's number sense in China and Finland. Scandinavian Journal of Educational Research, vol. 50, n.5, 483-502.
Baillargeon, R. (1994). Physical reasoning in young infants: seeking explanations for impossible events. British Journal of Developmental Psychology, vol.12, n.1, 9-33.
BAROODY, A. (2000). El pensamiento matemático de los niños. Madrid: Visor Distribuciones.
Barrouillet, P. y Camos, V. (2002). Savoirs, savoir-faire arithmétiques, et leurs deficiencies. Paris: Rapport pour le Ministère de la Recherche.
Berch, D. B. (2005). Making Sense of Number Sense: Implications for Children with Mathematical Disabilities. Journal of Learning Disabilities, vol.38, n.4, 333-339.
Bermejo, V. (1994). Conservaciones e invariantes cognitivos en el desarrollo. Aspectos psicológicos y epistemológicos. Estudios de Psicología, n.17, 80-92.
Brannon, E. (2002). The development of ordinal numerical knowledge in infancy. Cognition, vol. 83, 223-240.
Bryant, P. y Nunes, T. (2002). Children's understanding of mathematics. Blackwell handbook of childhood cognitive development. Ed. Goswami, Malden: The Netherlandsm Blackwell Publishing, 412-439.
Byrnes, J. y Wasik, B. (2009). Factors predictive of mathematics achievement in kindergarten, first and third grades: An opportunity–propensity analysis. Contemporary Educational Psychology, vol. 34, 167–183.
Caballero, S. (2005). Un estudio transversal y longitudinal sobre los conocimientos informales de las operaciones aritméticas básicas en niños de Educación Infantil. Tesis doctoral. Facultad de Psicología, Universidad Complutense de Madrid.
Cardoso, E. y Cerecedo, M. (2008). El desarrollo de las competencias matemáticas en la primera infancia en México. Revista Iberoamericana de Educación, vol.47, n.5, 5-25.
Cerda, G., Ortega, R., Pérez, C & Melipillán, R. (2010a). Inteligencia lógica y extracción social en estudiantes talentosos y normales de Enseñanza Básica y Media en Chile, Manuscrito enviado para publicación.
Cerda, G., Ortega, R., Pérez, C. & Flores, C. (2010b). Niveles de inteligencia lógica, rendimiento en matemáticas y factores asociados, en estudiantes chilenos. Manuscrito enviado para publicación.
Chen, R. y Walsh, V. (2009). Numerical representation in the parietal lobes: Abstract or not abstract? Behavioral and Brain Sciences, vol. 32, 313-328.
Clarke B. y Shinn, M. (2004) A preliminary investigation into the identification and development of early mathematics curriculum-based measurement. School Psychology Review, vol. 33, n. 2, 234-248.
Clements, D. H. (1984). Training effects on the development and generalization of Piagetian logical operations and knowledge of number. Journal of Educational Psychology, vol.76, n.5, 766-776.
Cowan, R., Foster, C. Y Al-Zubaidi, A. (1993). Encouraging children to count. British Journal of Developmental Psychology, vol. 11, n. 4, 411-420.
Donoso, S. Y Hawes, G. (2002). Eficiencia escolar y diferencias socioeconómicas: a propósito de los resultados de las pruebas de medición de la Calidad de la Educación en Chile. Educação e Pesquisa, vol. 28, n. 2, 25-40.
Ee, J., Wong, K. y Aunio, P. (2006). Numeracy of Young Children in Singapore, Beijing & Helsinki. Early Childhood Education Journal, vol. 33, n. 5, 325-332.
Eyzaguirre, B. y Le Foulon, C. (2001). La Calidad de la Educación Chilena en Cifras. Estudios Públicos, vol. 84, 85-204.
Geary, D., Bailey, D., Littlefield, A., Wood, P., Hoard, M. y Nugent, L. (2009). First-grade predictors of mathematical learning disability: A latent class trajectory analysis. Cognitive Development, vol.24, n.4, 411–429.
Gelman, R. y Gallistel, C. (1978). The child's understanding of number. Cambridge: HUP.
Gersten, R., Jordan, N. y Flojo, J. (2005). Early Identification and Interventions for Students with Mathematics Difficulties. Journal of Learning Disabilities, vol. 38, n. 4, 293-304.
Hernández, R., Fernández, C. y Baptista, P. (2006). Metodología de la investigación. México: McGraw-Hill Interamericana.
Howell, S. y Kemp, C. (2005) Defining Early Number Sense: A participatory Australian study. Educational Psychology, vol. 25, n. 5, 555-571.
Hyde, J., Fennema, E. Y Lamon, S. (1990) Gender differences in mathematics performance: a meta-analysis. Psychological Bulletin, vol. 107, n. 2, 139-155.
Jordan, N. , Kaplan, D., Locuniak, M. Y Ramineni, C. (2007) Predicting first-grade math achievement from developmental number sense trajectories. Learning Disabilities Research & Practice, vol. 22, n. 1, 36-46.
Jordan, J., Mulhern, G. Y Wylie, J. (2009) Individual differences in trajectories of arithmetical development in typically achieving 5- to 7-year-olds. Journal of Experimental Child Psychology, vol. 103, n. 4, 455–468.
Klein, P., Adi-Japha, E. Y Hakak-Benizri, S. (2010) Mathematical thinking of kindergarten boys and girls: Similar achievement, different contributing processes. Educational Studies in Mathematics, vol. 73, n. 3, 233-246.
Krajewski, K. Y Scheneider, W. (2009) Exploring the impact of phonological awareness, visual–spatial working memory, and preschool quantity–number competencies on mathematics achievement in elementary school: findings from a 3-year longitudinal study. Journal of Experimental Child Psychology, vol. 103, n. 4, 516–531.
Kroesbergen, E., Van Luit, J, Van Lieshout, E., Van Loosbroek, E. Y Van De Rijt, B. (2009) Individual differences in early numeracy: The role of executive functions and subitizing. Journal of Psychoeducational Assessment, vol. 27, n. 3, 226-236.
Lehalle, H. Connaissances numériques et modèles de développement. En J. Bideaud y H. Lehalle (eds.), Le développement des activités numériques chez l'enfant (pp. 29-54). Paris: Lavoisier,.
Lembke E. Y Foegen, A. (2009) Identifying early numeracy indicators for kindergarten and firstgrade students. Learning Disabilities Research and Practice, 2009, vol.24, n.1, 12-20.
Leseman, P. (2002). Early Childhood Education and care for children from low-income or Minority Backgrounds. Paris: OECD.
Locuniak, M. y Jordan, N. (2008) Using kindergarten number sense to predict calculation fluency in second grade. Journal of Learning Disabilities, vol. 41, n. 5, 451-459.
Mazzocco, M. y Thompson, R. (2005) Kindergarten predictors of math learning disability. Learning Disabilities Research and Practice, vol. 20, n. 3,142-155.
Mcewan, P. y Carnoy, M. (2000) The Effectiveness and Efficiency of Private Schools in Chile's Voucher System. Educational Evaluation and Policy Analysis, vol. 22, n. 3, 213-239.
Mella, O. (2003) 12 años de reforma educacional en Chile. Algunas consideraciones en torno a sus efectos para reducir la inequidad. REICE. Revista Electrónica Iberoamericana sobre Calidad, Eficacia y Cambio en Educación, vol.1, n.1 Disponible en http://www.ice.deusto.es/rinace/reice/Vol1n1/Mella.pdf.
Methe, S., Hintze, J. y Floyd, R. (2008) Validation and decision accuracy of early numeracy skill indicators. School Psychology Review, vol. 37, n. 3, 359-373.
Milicic, N y Schmidt, S. (2008). Prueba de precálculo: para evaluar el desarrollo matemático en niños de 4 a 7 años. Santiago: Universitaria.
MINISTERIO DE EDUCACIÓN. (2001). Bases Curriculares para la Educación Parvularia. Santiago: Unidad de Currículum y Evaluación.
MINISTERIO DE EDUCACIÓN. (2004). Chile y el aprendizaje de las matemáticas según TIMSS: Resultado de los estudiantes chilenos de 8° básico en el estudio internacional de tendencias en matemáticas y ciencias 2003. Santiago: Unidad de Currículum y Evaluación.
MINISTERIO DE EDUCACIÓN. PISA 2006. (2007a). Rendimientos de estudiantes de 15 años en Ciencias, Lectura y Matemática. Unidad de Currículum y Evaluación. Santiago de Chile: MINEDUC.
MINISTERIO DE EDUCACIÓN. (2007b). Niveles de Logro 4º Básico Lectura y Educación Matemática SIMCE. Unidad de Currículum y Evaluación. Santiago de Chile: MINEDUC.
MINISTERIO DE EDUCACIÓN. (2007c). Niveles de Logro 2º medio Lenguaje y Comunicación y Educación Matemática SIMCE. Unidad de Curriculum y Evaluación. Santiago de Chile: MINEDUC.
MINISTERIO DE EDUCACIÓN. (2009). Análisis de las competencias en NB1: caracterización de los niveles de complejidad de las tareas matemáticas. Santiago de Chile: MINEDUC.
Mizala, A. y Romaguera, P. (2000). School Performance and Choice: The Chilean experience. Journal of Human Resources, vol. 35, n. 2, 392-417.
Navarro, J., Aguilar, M., Alcalde, C., Marchena, E., Ruiz, G., Menacho, I. y Sedeño, M. (2009) Estimación del aprendizaje matemático mediante la versión española del Test de Evaluación Matemática Temprana de Utrecht. European Journal of Education and Psychology, vol.2, n.2., 131-143.
Navarro, J., Aguilar, M., Marchena, E., Alcalde, C. y García, J. (2010). Evaluación del conocimiento matemático temprano en una muestra de 3º de Educación Infantil. Revista de Educación, vol. 352, 601-615.
Niss, M. (1999). Competencies and Subject Description. Uddanneise, vol. 9, 21-29.
Nunes, T. Y Bryant, P. (1996). Children doing mathematics. Oxford: Blackwell.
Okpala, C. Y Okpala, A. (2001) Parental Involvement, Instructional Expenditures, Family Socioeconomic Attributes, and Student Achievement. The Journal of Educational Research, vol. 95, n. 2, 110-115.
Piaget, J. (1967). La génesis de las estructuras lógicas elementales. Buenos Aires: Guadalupe.
Piaget, J. (1965). The child's conception of number. New York: W.W. Norton.
Ramírez, M. (2006) Understanding the Low Mathematics Achievement of Chilean Students: A Cross-National Analysis Using TIMSS Data. International Journal of Educational Research, vol.45, n.3, 102-116.
Ramírez, M. (2007). Diferencias dentro de la Sala de Clases. Distribución del Rendimiento en Matemáticas. Estudios Públicos, vol. 106, 5-22.
Resnick, L. B. (1989). Developing mathematical knowledge. American Psychologist, vol. 44, n.2, 162-169.
Rico, L. (2007). La competencia matemática en PISA. PNA: Revista de Investigación en Didáctica de la Matemática, vol. 1, n. 2, 47-66.
Rico, L. y Lupiánez, J. (2008 ). Competencias matemáticas desde una perspectiva curricular. Madrid: Alianza Editorial.
Sarnecka, B. y Carey, S. (2008). How counting represents number: What children must learn and when they learn it. Cognition, vol. 108, 662-674.
Ségure, T., Del Solar, M. y Riquelme, G. (1994). Características Psicosociales de Alumnos de Educación Media en la Octava Región y su Incidencia en el Rendimiento Escolar. Revista de Educación Paideia, vol. 19, 37-44.
Starkey, P. Y Cooper, R. G. (1980). Perception of number by human infants. Science, vol. 210, 1033-1035.
Stock, P., Desoete, A. y Roeyers, H. (2009). Predicting arithmetic abilities: The role of preparatory arithmetic markers and intelligence. Journal of Psychoeducational Assessment, vol. 27, n. 3, 237-251.
Swanson. H. (2006). Cognitive processes that underlie mathematical precociousness in young children. Journal of Experimental Child Psychology, vol.9 3, n. 3, 239–264.
Torbeyns, J., Van Den Noortgate, W., Ghesquière, P., Verschaffel, L., Van De Rijt, B. y Van Luit, J. (2002). The development of early mathematical competence of 5- to 7-year-old children: A comparison between Flanders and The Netherlands. Educational Research and Evaluation, vol. 8, 249-275.
Treviño, E. y Donoso, F. (2010). Agrupación de escuelas para intervenciones de política: análisis del caso chileno. Facultad de Educación, Universidad Diego Portales. Disponible en http://www.cpce.cl/descargas/agrupacion_de_escuelas_para_intervencion_de_politica_julio_29_2010.pdf.
Uller, C., Carey, S., Huntley-Fenner, G. y Klatt, L. (1999). What representations might underlie infant numerical knowledge. Cognitive Development, vol.14, n.1, 1-36.
Van Luit, J., Van De Rijt, B. y Pennings, A. (1994). Utrechtse Getalbegrip Toets [The Utrecht Numeracy Test]. Doetinchem: Graviant.
Van De Rijt, B. (1996). Early mathematical competence among young children. Doetinchem: Graviant.
Van De Rijt, B. Y Van Luit, J. (1998). Effectiveness of the Additional Early Mathematics program for teaching children early mathematics. Instructional Science, vol. 26, n. 5, 337-358.
Van De Rijt, B., Van Luit, J. Y Pennings, A. (1999). The construction of the Utrech Early Mathematical Competence Scales. Educational and Psychological Measurement, vol. 59, n. 2, 289-309.
Willms, J. y Jacobsen, S. (1990). Growth in mathematics skills during the intermediate years: sex differences and school effects. International Journal of Educational Research, vol. 14, 157-174.
Woolfolk, A. (2006). Psicología Educativa. México: Pearson.
Woolley, M., Grogan-Kaylor, A., Gilster, M., Karb, R., Gant, L., Reischl, T. y Alaimo, K. (2008). Neighborhood social capital, poor physical conditions, and school achievement. Children & Schools, vol. 30, n. 3, 133-145.
Wynn, K., Bloom, P. y Chiang, W. (2002). Enumeration of collective entities by 5-month-old infants. Cognition, vol. 83, n. 3, 55-62.