Estudios Pedagógicos XXXVIII, Nº 2: 69-84, 2012

INVESTIGACIONES

Modelo Estocástico de las interconexiones conceptuales en un proceso de aprendizaje en el aula

Stochastic Model of the conceptual interconnections in a classroom learning process

Modelo estocástico de interconexões conceituais em processo de aprendizagem em sala de aula

José Alejandro González Campos, ^a Diana Milena Galvis Soto, ^b Juan Carlos Medina Magdaleno, ^c Nicolás Alberto Moreno Reyes ^c

^a Equipo Laboratorio [EXPERIMENTAL] de Saberes Matemáticos, Departamento de Matemática & Física, Facultad de Ciencias Naturales & Exactas, Universidad de Playa Ancha / Valparaíso, Chile. Valparaíso-Chile: E-mail: labesam.upla@gmail.com.
^b Facultad de Ciencias Básicas y Tecnología, Universidad del Quindío, Colombia, Bolsista da CAPES-IEL Nacional-Brasil.
^c Facultad de Ciencias Naturales & Exactas, Universidad de Playa Ancha, Valparaíso, Chile.

RESUMEN

Actualmente la inclusión es un concepto que está en la mesa de diálogo de las instituciones preocupadas por la educación, hacer parte del proceso de enseñanza y aprendizaje a todos los alumnos como personas, independiente de su realidad [3]. Sin embargo, el proceso de cuantificación y modelación de las interconexiones conceptuales, es un proceso distante, por tal razón, queremos dar un paso adelante en una educación para todos y objetivizar los procesos de cuantificación de la consistencia grupal en torno a un concepto [1], que denominaremos inclusión cognitiva. Por tal razón se definen los Grafos de Consistencia Conceptual (GCC) y el vínculo conceptual como una variable aleatoria Poisson, promoviendo una metodología de visualización y cuantificación de la Consistencia Conceptual de grupo. Este trabajo tiene como base teórica el procesamiento de los saberes según el Laboratorio Experimental de Saberes Matemáticos, Lab[e]saM [1] y se trasforma en un nuevo complemento para el estudio de las trasposiciones didácticas.

Palabras clave: saberes, grafos, matriz de adyacencia, distribución Poisson, intervalos de confianza, distribución asintótica.

ABSTRACT

Currently inclusion is a concept present in the dialogue of the institutions concerned about education; it means to include in the teaching-learning process all students as individuals, regardless of their reality [3]. However, quantification and modelling of conceptual interconnections is a distant process; therefore, our intention is to take a step forward an education for all, and objectify the quantification process in group consistency around a concept [1] which will be called cognitive inclusion. Therefore, conceptual consistency graph and conceptual link are defined as a Poisson random variable, promoting a visualization and quantification methodology of conceptual consistency within a group. This paper is based on the knowledge processing according to the LAB[e]SAM [1] and it turns into a new complement for the transposition didactics studies.

Key words: knowledge, graph, adjacency matrix, Poisson distribution, confidence interval and asymptotic distribution.

RESUMO

Inclusão, na atualidade, é um conceito amplamento discutido nas instituições de ensino que se preocupam com o processo ensino-aprendizagem de todos os estudantes como pessoas, independentemente do contexto em que se inserem [3]. No entanto, o processo de quantificação e modelagem das interconexões conceituais, é um processo distante da realidade esperada. Assim, dá-se um passo à frente na educação para todos e objetiva-se os processos de quantificação da consistência grupal em torno de um conceito [1], denominado inclusão cognitiva. Por essa razão, definem-se Gráficos de Consistência Conceitual (GCC) e o vínculo conceitual como uma variante aleatória Poisson, promovendo uma metodologia de visualização e quantificação da consistência conceitual grupal. Baseia-se em processamento de saberes segundo o Laboratório Experimental de Saberes Matemáticos, Lab[e] saM [1] que se transformam em novo complemento para o estudo das transposições didáticas.

Palavras chave: saberes, gráficos, matriz de adjacência, distribuição de Poisson, intervalos de confiança e distribuição assintótica.

1. INTRODUCCIÓN

Actualmente en el ámbito de la evaluación educacional se está interesado en determinar con mayor precisión el nivel de competencias de nuestros alumnos [2], sin embargo, desde el punto de vista del educador, ya no sólo interesa el logro individual en torno a un concepto, sino que además, si dicha construcción teórica es consistente con la de sus pares, es decir se quiere una perspectiva integral del curso.

En el proceso de visualización y cuantificación estocástica de la inclusión cognitiva, se considera la existencia de un instrumento de evaluación con todas las características edumétricas deseables, como por ejemplo fiabilidad y validez, pues dependerá de ello la potencia de las conclusiones del análisis.

Desde la perspectiva estocástica, se recurrirá a la distribución Poisson, que vendrá a caracterizar el comportamiento de la representación gráfica del Grafo de Consistencia Conceptual.

2. EL PROBLEMA DE INVESTIGACIÓN

En la actualidad el uso de la tecnología ha permitido desarrollar una serie de estrategias metodológicas para la medición del logro de una competencia, como por ejemplo la Teoría de Respuesta al ítem y la incorporación del tiempo de respuesta[2], sin embargo son visiones orientadas al alumno de manera individual, lo que definitivamente se convierte en una muestra poco significativa y no sujeta a generalización, lo que, como profesor, limita la auto evaluación y la reestructuración de los métodos de enseñanza o trasposiciones didácticas, es por esto que nos interesa una visualización grupal del concepto [5], de tal manera de capturar la arquitectura conceptual producto de la intervención pedagógica, de manera robusta y libre de sesgos individuales.

Por tal razón, el problema de este trabajo es: "Estructurar y formalizar una metodología de Visualización y cuantificación estocástica de la Inclusión Cognitiva".

3. OBJETIVOS DE LA INVESTIGACIÓN QUE SE PRESENTA

• Promover un método de visualización y cuantificación estocástica de la inclusión cognitiva.
• Describir y Caracterizar los Grafos de Consistencia Conceptual (GCC).
• Definir una estructura teórica de la Inclusión Cognitiva y su sustento formal en la visualización.
• Formalizar intervalos de Confianza para la cuantificación de la Inclusión Cognitiva.
• Promover una línea de investigación en torno a los GCC

4. METODOLOGÍA DE LA INVESTIGACIÓN

La metodología de trabajo, es de tipo exploratoria, en el sentido del comienzo de un nuevo eje de investigación en el que pretendemos asentar las bases teóricas, supuestos y restricciones de la metodología de análisis de la Inclusión Cognitiva y los Grafos de Consistencia Conceptual.

Este trabajo toma como base la concepción teórica de los saberes según Lab[e]saM[1].

Fases de la Investigación:

1. Análisis preliminar.
2. Concepción de la investigación.
3. Simulaciones.
4. Análisis a posteriori y evaluación.

5. ALGUNOS ANÁLISIS PRELIMINARES

La concepción teórica Lab[e]saM está soportada por el marco de la Teoría de las Situaciones Didácticas (Brousseau, 2004), y particularmente en la aproximación antropológica propuesta por Chevallard (1991), caracterizando así tres facetas:

• Saber Sabio generado en las comunidades científicas. Para esta investigación consideraremos que el saber Sabio posee infinitas dimensiones¹ no manejables en el sentido estadístico.
• Saber a Enseñar se orienta a la labor del enseñante (i.e., el que enseña) que debe producir la recontextualización y elección responsable de los conocimientos que pretenden transformarse en conocimiento para el alumno, es decir la labor del enseñante es elegir y construir un modelo (y como tal, reduce la complejidad) adecuado al contexto y al saber sabio, para transformarlo en un saber adecuado para enseñar.
• Saber Aprendido, representa el modelo construido por el alumno como producto del trabajo intelectual en su interacción con el modelo enseñado.

Pensamos que, a través de este trabajo, podemos iniciar un camino hacia la caracterización de las variables que tienen mayor incidencia en el modelo que el alumno construye en una situación de enseñanza, y en la calidad de éste, sin embargo el lineamiento teórico que aquí se describe está orientado al individuo y no de manera conjunta.

FORMALIZACIÓN:

Sean Θ el universo de los saberes sabios, donde cada θ ∈ Θ tiene asociado un conjunto X_θ constituido por todas las dimensiones de θ, que suponemos es de tamaño no finito, y

donde 2^X_θ es la familia de las partes de X_θ . Además sea; Ψ : Θ → una aplicación que denominaremos Operador de Elección donde la imagen de θ ∈ Θ, a través de Ψ, elige un subconjunto finito y no vacío de X_θ que se espera caracterice a θ.

Observemos que es una σ — álgebra sobre {X_θ : θ ∈ Θ}. Por otro lado se define un Operador de Transposición Γ, cuyo dominio es , una familia de conjuntos finitos de , esto es ⊂ , cuyas proyecciones definen, una familia de saberes enseñados, que a través de un proceso de decodificación el alumno lo transforma en saber aprendido.

Esta familia de saberes aprendidos, W, contiene algunas dimensiones y seudo-dimensiones² del saber cuya #W ≤ #, según lo anterior, interesa determinar cuáles fueron aquellas dimensiones que constituyen a W que son parte de , además determinar qué tan distante se encuentran estas seudo-dimensiones de lo que debieran haber sido y, por último, cuál es la distancia existente entre el saber aprendido y saber a enseñar, es decir, cual es la distancia entre el modelo definido por el alumno a través de la transposición (saber aprendido) y el saber a enseñar.

Adviértase que si #W ≥ #Ψ(Ω), la distancia entre el saber aprendido y el saber a enseñar se considerará nula.

Visualización:

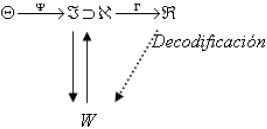Los aspectos antes detallados permite visualizar el contexto de las trasposiciones didácticas pero miradas en función de la individualidad, es decir como el proceso de transposición afecta a los individuos pero de manera particular [6], es decir, para un alumno X la transposición T permitió que el modelo desarrollado por el alumno, saber aprendido, fuese muy parecido al saber a enseñar, por otro lado, la misma transposición T en un alumno Y puede tener consecuencias desastrosas.

5.1 EL CONCEPTO DE GRAFO Y SUS RESTRICCIONES

Un Grafo G es un par (V, E) donde V es un conjunto finito no vacío de objetos llamados vértices y E es un conjunto (posiblemente vacío) de pares no ordenados de vértices distintos de G llamados aristas o líneas. El conjunto de vértices de G es denotado por V(G), mientras que el conjunto de aristas o líneas es denotado por E(G). Si e= {u, v} es una arista o línea de un grafo G, entonces u y v son vértices adyacentes, mientras que u y e son incidentes, como lo son v y e. Además, si e₁ y e₂ son aristas distintas de G incidentes con un vértice común, entonces e₁ y e₂ son aristas adyacentes. De aquí en adelante, denotaremos una línea por uv o vu en lugar de {u,v}.

La cardinalidad del conjunto de vértices de un grafo G es llamado el orden de G y es denotado por p(G) , o más simple, p, y la cardinalidad del conjunto de aristas es el tamaño de G y es denotado por o q(G) . Un grafo (p, q) tiene orden p y tamaño q.

Es costumbre definir o describir un grafo por medio de un diagrama en el que cada vértice es representado por un punto y cada arista e = uv es representado por un segmento de la línea o curva que une los puntos que corresponden a u y v.

Un grafo G, con conjunto de vértices V (G) = {v₁, v₂,...,v_p } puede ser también descrito por medio de matrices. Así A(G) = [ a_ij], donde

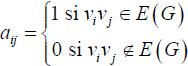Que es llamada matriz de adyacencia del Grafo G

Otra forma de representar a un grafo es a través de la matriz de incidencia. Así

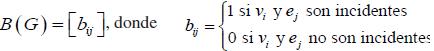Otro concepto a destacar en la teoría de grafos, es el grado de un vértice v en un grafo G, que es el número de aristas de G incidentes con v. El grado de un vértice v en G es denotado deg_G v o simplemente deg v , que en este trabajo será representado por X. Un vértice es llamado par o impar si el grado es par o impar. Un vértice de grado 0 en G es llamado vértice aislado y un vértice de grado 1 es un vértice final de G.

Grafo Completo: Para un número de vértices n, con n ≥ 1, el número máximo de aristas o líneas que se pueden definir es que caracteriza al grafo completo, designado por K_n [4].

5.2. EL MODELO POISSON Y SUS PROPIEDADES ASINTÓTICAS

Si X es una variable aleatoria, definida como el número de eventos que ocurren por unidad de tiempos (espacio, volumen, etc.), entonces se prueba que bajo ciertos supuestos:

Entonces el estimador Máximo Verosímil del parámetro λ es , que como consecuencia del Teorema Central del Límite, su distribución asintótica es:

, a partir de la cual podemos definir el siguiente pivote.

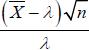cuya distribución normal estándar, es decir:

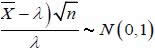Luego un intervalo de confianza para λ del ( 1 - α) 100% es:

6. PROPUESTA

Sea M una matriz de respuestas de orden pxn, donde p representa el número de ítems de una prueba, la cual se asume posee buenas características edumétricas y n el número de personas sometidas a esa prueba, por lo tanto cada columna está compuesta por la cuantificación numérica de las puntuaciones de una persona en cada ítem de la prueba.

Posteriormente nos interesa como la arquitectura conceptual de cada alumno se asimila o cohesiona con la de sus pares en la misma prueba, lo que será cuantificado con el coeficiente de Correlación de Pearson, de esta forma se da origen a una matriz cuadrada de orden n, [ρ_ij] donde [ρ_ij] representa la correlación entre las puntuaciones de la persona i con la persona j en la prueba. A partir de la matriz de correlación, [ρ_ij] se define la matriz de Consistencia, que es una variación de la anterior en la cual los son considerados iguales a cero, que para evitar confusiones la denominaremos C = [ρ_ij].

C = [ρ_ij] es una matriz simétrica, cuyas componentes de la diagonal principal son ceros.

De entre los coeficientes de la matriz de Consistencia, nos interesan todos aquellos que representen una dependencia significativa, como por ejemplo

Sea C = [ρ_ij] una matriz de Consistencia y A = [a_ij] la matriz de adyacencia, donde

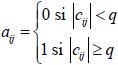donde q es el umbral de corte, luego si a_ij = 0 entonces no existe vinculo o consistencia entre la persona i con la persona j, si entonces existe vinculo o consistencia entre la concepción teórica de la persona i con la persona j.

Definición: Un Grafo de Consistencia Conceptual (GCC), es un grafo, en el cual sus vértices son las personas que rindieron una prueba y las aristas o líneas representan la existencia de Consistencia Conceptual entre las personas involucradas, que se visualizarán si a_ij = 1 .

Definición: El Grado de un vértice v de un Grafo de Consistencia Conceptual, es el número de aristas o líneas del GCC incidentes con v, que lo representaremos por X.

Bajo esta concepción, el grado de un Vértice v o simplemente X, es una variable aleatoria modelada por la distribución Poisson, pues estamos contando el número de aristas incidentes en el vértice v, que es un modelo estocástico para la cuantificación de la inclusión cognitiva, que en este caso está representada por λ.

Es decir

partir de la cual podemos definir el siguiente pivote.

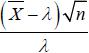cuya distribución es normal estándar, es decir:

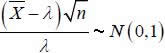Luego un intervalo de confianza para λ del ( 1 — α) 100% es:

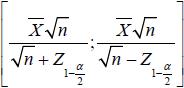Este intervalo viene a caracterizar de manera cuántica al grupo de personas, en cuanto a sus vínculos conceptuales, además de permitir el contraste con otros grupos o cursos.

7. SIMULACIONES

Sea M una matriz de respuestas de orden 10 x 30, donde 10 es el número de ítems de una prueba identificados por las filas y 30 el número de personas sometidas a esa prueba identificadas con las columnas, por lo tanto cada columna está compuesta por la cuantificación numérica de las puntuaciones de una persona en cada ítem de la prueba, como se muestra en la siguiente tabla.

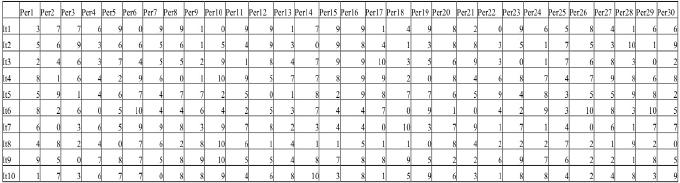Tabla 1

La tabla 1 contiene simulaciones de las puntuaciones de 30 alumnos a una prueba de 10 preguntas. Debemos destacar que no es necesario que las puntuaciones estén en esta escala (0-10), la única exigencia es que el estatus métrico de las puntuaciones sea cuantitativo o usar otro tipo de correlación, como por ejemplo Spearman.

Posteriormente nos interesa como la arquitectura conceptual de cada alumno se asimila o cohesiona con la de sus pares en la misma prueba, lo que será cuantificado con el coeficiente de Correlación de Pearson, de esta forma se da origen a una matriz cuadrada de orden 30, donde cada componente representa la correlación entre las puntuaciones según cada subíndice.

A partir de la matriz de correlación, [ρ_ij], se define la matriz de Consistencia, C = [c_ij]. es C = [c_ij] una matriz simétrica, cuyas componentes de la diagonal principal son ceros.

De entre los coeficientes de la matriz de Consistencia, nos interesan todos aquellos que representen una dependencia significativa, que en esta simulación utilizaremos como punto de corte o umbral |c_ij| ≥ 0,5, es decir si C = [c_ij] una matriz de Consistencia A = [a_ij] y la matriz de adyacencia, cada componente queda definido por

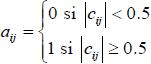Luego si a_ij = 0 entonces no existe vinculo o consistencia entre la persona i con la persona j a un nivel mayor a 0.5, si a_ij = 1 entonces existe vinculo o consistencia entre la concepción teórica de la persona i con la persona j.

La matriz de Consistencia y de adyacencia son las siguientes:

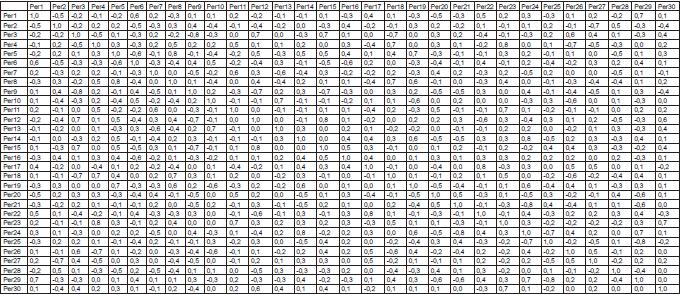Tabla 2

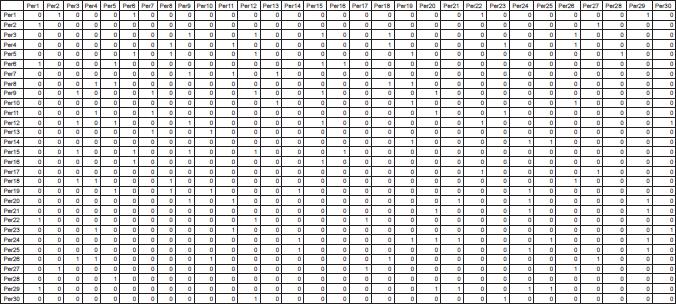Tabla 3

Grafo de Consistencia Conceptual, para representar el GCC, es necesario identificar que componentes de la matriz de Adyacencia son iguales a 1, es decir a_ij = 1 , a partir de ello, se tiene:

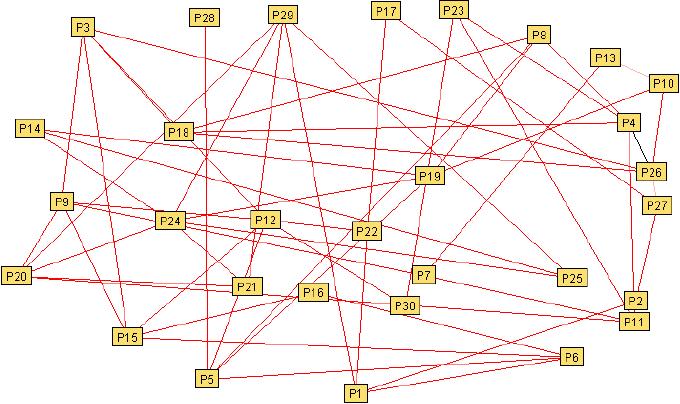Gráfico 1

Observemos que en la medida que el GCC converge al grafo completo, la consistencia conceptual se incrementa, lo que se traduce en un método de decisión respecto de la elección de la transposición didáctica. Por otro lado el Grado de los vértices del Grafo de Consistencia Conceptual, X, tiene la siguiente distribución de frecuencias.

Gráfico 2

Que es modelada por la distribución Poisson, que al utilizar propiedades asintóticas de los estimadores de λ o en nuestro contexto, de la inclusión cognitiva, se desprenden los resultados siguientes:

Un intervalo de confianza para λ del ( 1 — α) 100% es:

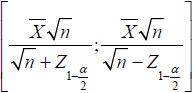en nuestro ejemplo y considerando α = 0,05, se tiene que el intervalo de confianza para la consistencia cognitiva del grupo en cuestión es:

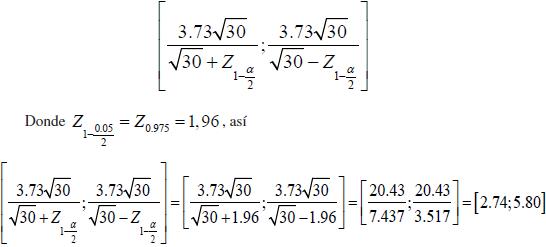Este intervalo viene a caracterizar de manera cuántica al grupo de personas, en cuanto a sus vínculos conceptuales, además de permitir el contraste con otros grupos o cursos.

De manera similar, simularemos otra prueba, en la cual el Grafo de Consistencia Conceptual, es:

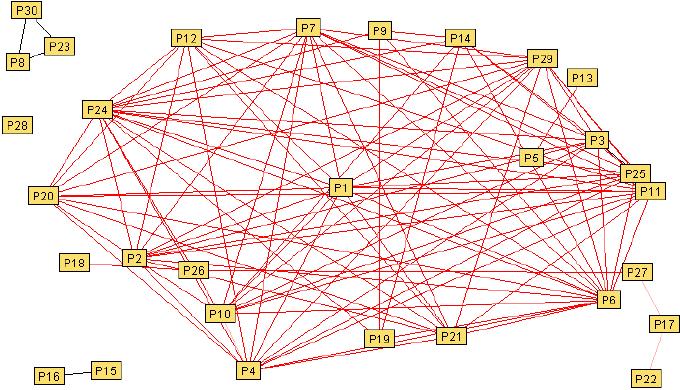Gráfico 3

No es complejo observar las diferencias entre los dos grupos, pues aquí definitivamente el número de conexiones o aristas es mayor y la convergencia al grafo completo es más clara, por lo tanto la consistencia conceptual es mayor, lo que permite una comparación de las transposiciones didácticas.

Nuevamente utilizando α = 0,05 , se tiene que el intervalo de confianza para la consistencia cognitiva del grupo en cuestión es:

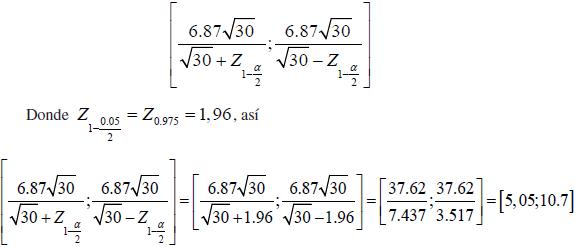8. ANÁLISIS A POSTERIORI Y EVALUACIÓN

Definitivamente, la cuantificación del segundo grupo permite definir un intervalo con una amplitud mucho mayor y con cotas más extremas, es decir la inclusión cognitiva de este grupo es mayor que la del grupo anterior.

Además al realizar un contraste de igualdad de medias, esta es rechazada, es decir no podemos asumir que tienen igual media, por lo tanto y de manera equivalente no podemos asumir que las cuantificaciones de la inclusión cognitiva en los grupos sean igual.

9. CONCLUSIONES

La propuesta que aquí hemos desarrollado, abre una línea de investigación y desarrollo en beneficio de caracterizar las transposiciones didácticas, que en este primer paso, se estructuran las bases de un lenguaje formal, en el que interactúan procesos estocásticos y desarrollos determinísticos, llevándonos a una visualización y caracterización de la consistencia cognitiva.

Los desafíos pendientes se orientan a la cuantificación la distancia entre el saber a enseñar y el saber aprendido, pero en contexto de grupo. Por otro lado a caracterizar los grafos de consistencia conceptual.

10. AGRADECIMIENTOS

A mi esposa, Paula Sofía Ponce Grenet.

NOTAS

¹ En este trabajo el sustantivo dimensión alude a cada una de las características esenciales del saber.

² En este caso utilizamos la palabra seudodimensión para hacer alusión a la dimensión de saber que posee el alumno, y que no coincide con las dimensiones del saber enseñado que recibió.

REFERENCIAS BIBLIOGRÁFICAS

Cabrera, E.; González, J. et al. (2010). Una didáctica del saber: un camino hacia la optimización de las transposiciones didácticas. Estud. pedagógicos, vol. 36, n. 2, 51-61.

Cabrera, E.; González, J. et al. (2010). Test informatizados y el registro del tiempo de respuesta, una vía para la precisión en la determinación del nivel de logro de un saber matemático. Estud. pedagógicos, 2010, vol. 36, n. 1, 69-84.

Infante, M. (2010). Desafíos a la formación docente: inclusión educativa. Estud. pedagógicos, vol. 36, n. 1, 287-297.

Montenegro, E., González, J. et al. (2010). Graphs r-Polar Spherical Realization. Proyecciones, vol. 29, n. 1, 31-39.

Rocha, M. Lopes da. (2008). Inclusão ou exclusão? Produção de subjetividade nas práticas de formação. Psicologia em estudo, vol. 13, n. 3, 477-484.

Toro Fuenmayor, L. (2006). Educación superior: inclusión y exclusión: Calidad con equidad y equidad con calidad. Educere, vol. 10, no. 33, 369-378.