INVESTIGACIONES

Una propuesta para el desarrollo de modelos geométricos en las Educadoras de Párvulos. El caso del polígono

A proposal for the development of geometric models in Preschool Teachers. The case of polygons

Uma proposta para desenvolvimento de modelos geométricos nas educadoras de infância. O caso do poligono

Astrid Morales S.,^a Lorena Rosas T.^b

^a Pontificia Universidad Católica de Valparaíso Telf.: (32)2274063. Correo electrónico: astrid.morales@pucv.cl
^b Universidad Tecnológica de Chile, INACAP, Santiago Correo electrónico: lorenarosast@gmail.com

RESUMEN

El desarrollo del pensamiento matemático en los párvulos es fundamental para enfrentar los desafíos de su desarrollo escolar; el tipo de experiencia que tengan con la matemática puede determinar su desempeño escolar futuro. Desafortunadamente, en Chile, la formación de educadores de párvulos en matemáticas se desarrolla en una forma tradicional y además débil. La investigación que presentamos muestra un camino viable de construcción de conocimiento geométrico en educadoras/es de párvulos, de manera tal que estas podrían replicarlo con sus propios estudiantes. El trabajo se desarrolla bajo la teoría Socioepistemológica; la argumentación gráfica ayuda la construcción de los modelos geométricos, en este caso, los polígonos.

Palabras clave: polígono, socioepistemología, resignificación, argumentación gráfica.

ABSTRACT

The development of Mathematical Thinking in preschool kids is essential for them to meet the challenges of their school development; the kind of mathematical experience that they get may determine their future school performance. Unfortunately, in Chile, mathematics nursery teacher training develops in a traditional and also weak form of teaching and learning. This paper shows a viable means of knowledge building in geometry for preschool teachers, in a way that they may replicate with their own students. The research is conducted under the Socioepistemologic theory; graphical argumentation helps in the building of geometric models, in this case, polygons.

Key words: polygon, socioepistemologic, resignification, graphical argumentation.

1. INTRODUCCIÓN

En la actualidad, el Ministerio de Educación, en concordancia con la evidencia empírica nacional e internacional, ha puesto énfasis en la importancia de extender la cobertura y asegurar la calidad de la Educación Preescolar. Una de las consecuencias de aquello es que el Segundo nivel de transición "kínder", hoy es obligatorio.

En términos de la formación, los profesores que están a cargo de educar a los pequeños de estos niveles son las educadoras de párvulos¹, que en la actualidad son formadas en institutos profesionales y universidades de la más amplia variedad en calidad de formación. Adicionalmente, los curriculum, ya sea en los institutos o universidades, poseen escasos cursos específicos de matemáticas (3 a 4 cursos a lo largo de toda la malla de 4 años en general). Más aún, estos cursos no están dirigidos a la especialidad, sino que corresponden a un curso típico de matemáticas que se dicta ya sea a nivel secundario o a nivel universitario, en donde el pensamiento matemático no se cuestiona ni se reflexiona al nivel correspondiente, si no se reduce a operatorias, fórmulas o simplemente a la contextualización de estos a la educación de la matemática, sin tener claras las nociones previas que se está trabajando.

1.1. ESCENARIO ACTUAL

La educación formal obligatoria en nuestro país contempla la introducción de las primeras nociones de matemática, específicamente de la geometría, a muy temprana edad. Con ello, las Bases Curriculares para la Educación Parvularia (MINEDUC, 2001), contemplan su aparición desde el Primer Nivel de Transición (Prekinder) con estudiantes que no superan los 5 años de edad, lo cual obviamente significa un gran avance para la educación matemática de nuestro país.

Conscientes de que la calidad de los aprendizajes depende en gran parte de la calidad profesional y de la formación profesional de las personas encargadas del proceso de enseñanza-aprendizaje en estos niveles —foco de nuestra investigación— realizamos una revisión a los estándares para la formación de estudiantes de Pedagogía en Educación Parvularia (Ministerio de Educación [MINEDUC], 2012a), con el fin de dar a conocer los contenidos específicos de Geometría que debe cursar la educadora de Párvulos en el período de su formación profesional. Como también los Programas curriculares oficiales y textos de estudio de matemática otorgados por el Ministerio de Educación de Chile (MINEDUC, 2012b) para los estudiantes de Educación Preescolar (Primer y Segundo Nivel de Transición, hacia los 5 y 6 años de edad, respectivamente). Mencionaremos algunos aspectos de lo declarado.

1.1.1. Estándares orientadores para carreras de educación parvularia. Estándares pedagógicos y disciplinarios

Los Estándares Orientadores para carreras de Educación Parvularia (en adelante, EOEP) obedecen a la necesidad de fortalecer la educación durante la primera infancia, por lo que declaran que la mejora de la calidad de la educación está en directa relación con la calidad profesional de quienes enseñan en las aulas y, en consecuencia, con la formación que toda educadora de párvulos recibe durante sus estudios superiores (MINEDUC, 2012a). Los EOEP están divididos en dos partes, los estándares pedagógicos y los estándares disciplinarios y fueron creados en cierta medida con el fin de orientar a las instituciones de educación del país, para ajustar sus programas de formación de educadoras de párvulos, a objeto de que sus estudiantes alcancen los aprendizajes que estos determinan.

Con respecto a los estándares disciplinarios, existe uno relacionado con los conocimientos matemáticos que la educadora de párvulos debe alcanzar al ingresar al ejercicio de la Educación Parvularia, manejar estrategias pedagógicas basadas en su comprensión de las nociones fundamentales de las matemáticas. En geometría, comprender y manejar nociones teóricas fundamentales y elementos de la geometría: Figuras planas y figuras geométricas básicas, sus propiedades, su visualización y su medición. Sin embargo, creemos que esto no se está cumpliendo a cabalidad, dado que las estudiantes no tienen la suficiente cantidad de instancias en los cursos de formación para propiciar el desarrollo de su pensamiento matemático, puesto que la enseñanza de la matemática, en general y como se mencionó, no se cuestiona ni se reflexiona al nivel correspondiente, si no se reduce a operatorias, fórmulas o simplemente la contextualización de estos a la educación de la matemática, lo que no daría cabida a un aprendizaje de la naturaleza necesaria para poder transmitirlo a sus estudiantes.

1.1.2. Programas de estudio y textos para educación parvularia

Desde el punto de vista de la educación matemática, existe un único programa para cada nivel de educación parvularia, el que reúne todas las asignaturas, separadas por ámbitos. El aprendizaje esperado relacionado a la geometría es reconocer algunos atributos, propiedades y nociones de algunos cuerpos y figuras geométricas en dos dimensiones, en objetos, dibujos y construcciones, lo que requiere, como lo señalan los estándares, comprender y manejar nociones teóricas fundamentales y elementos de la geometría (MINEDUC, 2008), problema que aborda nuestra investigación.

En general, en los textos de estudio se observa que las secuencias didácticas de los conocimientos asociados a las nociones de la geometría de cada curso comienzan con una contextualización en la vida cotidiana donde se debe reconocer diversas formas geométricas, las que luego se estudian con más profundidad. Creemos que estas actividades son importantes para acercar el conocimiento a la vida de los estudiantes, sin embargo, creemos que no contribuyen a una verdadera construcción de conocimiento. Si queremos que los estudiantes valoren socialmente la matemática es necesario que la utilidad del conocimiento esté en sí mismo y no en sus aplicaciones, es por ello que para comenzar el estudio es necesario acudir a actividades donde el estudiante sea quien construya su conocimiento, tome datos, haga conjeturas y utilice sus conocimientos previos.

2. PROBLEMÁTICA DE INVESTIGACIÓN

La importancia y trascendencia de la Geometría es indudable, esta introduce al individuo al desarrollo del razonamiento deductivo y visualización de imágenes, que serán requeridos en otras ramas de las Matemáticas. En particular, la Geometría Euclidiana es considerada como fundamental, debido a que tiene como objeto desarrollar tempranamente el pensamiento espacial de los alumnos, por medio del reconocimiento, visualización y dibujo de figuras 3D y 2D (MINEDUC, 2012a, 2012b), necesario para la progresión del aprendizaje de otras ramas de la Geometría, como la Analítica, No Euclidiana, Diferencial y otros contenidos matemáticos.

Curricularmente, en la enseñanza Básica chilena, Geometría es el eje que cuenta con mayores dificultades, presentando el rendimiento más bajo en las mediciones nacionales e internacionales. Evidencia de lo anterior lo constituyen los resultados generales de la prueba (MINEDUC, 2004) que revelan que Geometría es menos enfatizada en el currículo que lo definido como adecuado internacionalmente. A raíz de situaciones como la mencionada, el Marco Curricular para la Educación Escolar experimenta continuos ajustes con el fin de mejorar la calidad de la educación. Estos apuntan a que el estudiante adquiera conocimientos, actitudes y habilidades que deben ser de utilidad para comprender el mundo que lo rodea, lo que claramente requiere de una matemática funcional, desde el punto de vista de la Teoría Socioepistemológica, es decir, un conocimiento incorporado orgánicamente al ser humano, que transforma su realidad; en oposición al conocimiento utilitario, carente de significados para el estudiante (Cordero, 2006). La funcionalidad permite que el conocimiento matemático adquiera significados dentro y fuera del ámbito escolar, lo que conlleva que el conocimiento matemático sea valorado por los estudiantes y no quede al nivel de aplicación de fórmulas que simplemente olvida y que no es capaz de extrapolar a otras situaciones. Sin embargo, creemos que el actual Discurso Matemático Escolar² (en adelante, dME) no está logrando la funcionalidad que se requiere en torno al conocimiento matemático, debido a que se privilegia los conceptos matemáticos por sobre las circunstancias que le dieron origen y que son, en definitiva, aquellas prácticas que posibilitan la adquisición de los mismos. Tal como lo señala Arrieta (2003), se presenta al conocimiento matemático como algo abstracto y acabado, carente de significado para el estudiante.

En los programas de estudio se menciona a la modelación como una de las habilidades para el desarrollo del pensamiento matemático. Sin embargo, creemos que la visión que se tiene de ella es muy distinta a lo que esperamos para lograr la resignificación³ del conocimiento. En las Bases Curriculares Educación Básica encontramos lo siguiente: "Modelar es considerado como el proceso de utilizar y aplicar modelos, seleccionarlos, modificarlos y construir modelos matemáticos, identificando patrones característicos de situaciones, objetos o fenómenos que se desea estudiar o resolver, para finalmente evaluarlos" (MINEDUC, 2012b: 3). La concepción anterior de la modelación es comprendida como una aplicación de la matemática, lo que implica, enseñar primero el conocimiento matemático y luego buscar una explicación de tal conocimiento (Cordero, 2006; Cordero, Cen y Suárez 2010). Contrariamente a esta idea, en nuestra investigación asumiremos a la modelación en el proceso de enseñanza y aprendizaje de las matemáticas como una práctica. La modelación, como lo señala Cordero, "tiene que ser algo más robusto que una representación o una aplicación matemática, tiene que ser una práctica plasmada específicamente como la argumentación de la situación en cuestión" (Cordero, 2006: 5).

A raíz de lo anterior, esta investigación pretende aportar con elementos que permitan la resignificación del polígono, sus elementos y propiedades, a través de la argumentación gráfica como hilo conductor de la construcción del conocimiento matemático (Morales et al., 2012). Todo ello con el fin de que el estudiante construya una base de conocimientos para progresar en el estudio de la Geometría.

El sustento teórico de esta investigación es la socioepistemología, la que a través de diversos resultados de investigación señala la conveniencia de hacer estudios del uso del conocimiento matemático y su desarrollo para crear un marco de referencia donde se resignifique a la matemática. Además, desarrollaremos la idea de que con la argumentación gráfica se desarrolla el pensamiento matemático y se construye conocimiento; se han realizado trabajos en torno a la gráfica de funciones, y hemos visto la pertinencia de ampliar la concepción de la gráfica a toda figura de la que se extrae información matemática.

En este sentido, los polígonos son gráficas y en esta investigación se plantea enfocar la atención a los argumentos que surgen de estas y que facilitan la construcción de conocimiento matemático, resignificando los polígonos en un proceso de modelación.

2.1. UNA MIRADA AL ESTATUS DEL PROCESO DE ENSEÑANZA Y APRENDIZAJE DE LOS POLÍGONOS EN EL DISCURSO MATEMÁTICO ESCOLAR

El proceso de enseñanza y aprendizaje de los polígonos se ha quedado en nivel utilitario, donde lo que se aprende en la escuela solo sirve en la clase de Geometría, no logrando alcanzar un nivel de funcionalidad que permita al estudiante extrapolar lo que allí se aprende a otros ambientes. Esto es debido a que en las clases se privilegia la aplicación de fórmulas memorizadas y sin significados, lo que trae como consecuencia que los procesos de visualización, argumentación y justificación no tengan un papel preponderante en la enseñanza de la disciplina (Ballestero y Gamboa, 2010). Es por ello que en esta investigación daremos cuenta del rol de las argumentaciones que emergen del uso de la figura, que permiten la construcción de conocimiento matemático en torno al polígono.

Tradicionalmente, las clases de Geometría se han basado en secuencias de aprendizaje que siguen el esquema: definiciones-teoremas-ejemplos-ejercicios de aplicación (Ballestero y Gamboa, 2010). Con lo cual se presentan las nociones a los estudiantes como un conjunto de definiciones, fórmulas y teoremas que no tienen ninguna relación con la realidad. Es decir, se ve a la Geometría Euclidiana como un producto acabado, carente de significados propios que se puedan construir y reconstruir. El estatus tradicional que se le da a las figuras geométricas —en particular de los polígonos— en los textos de estudio, está ligado al de representación de un enunciado o de aplicación de un contenido, dejando de lado, otros usos que podrían constituir nuevos marcos de referencia donde se resignifique a los polígonos. Creemos que el dibujo de las figuras geométricas no es utilizado para modelar y construir conocimiento. Es por ello que se pretende dotar de nuevo significado y así contribuir a su resignificación.

En las clases de Geometría comúnmente se observa que los estudiantes aprenden de memoria los elementos y propiedades de los polígonos, no logrando una comprensión de éstos. Además, según señala (Chamorro, 2007), se enseña la geometría de una forma ostensiva, de manera que el estudiante debe asumir que lo que se enseña es la verdad absoluta y el único trabajo que se le deja es el de aplicar los conocimientos aprendidos en la clase, por el contrario, creemos que el aportar con situaciones en las que las argumentaciones que derivan del convencimiento de unos estudiantes a otros sea necesario, permite que se resignifiquen algunas propiedades, elementos y los polígonos.

Godino et al. (2004) mencionan que en Geometría un problema didáctico es que con frecuencia se utiliza la misma palabra para referirse a objetos abstractos y objetos de la realidad concreta, dejando de lado la naturaleza geométrica de los mismos.

A raíz de los antecedentes antes mencionados, se asume como hipótesis de investigación que una situación de variación de los elementos de los polígonos, la argumentación gráfica en un contexto de modelación, permite la resignificación de los polígonos, logrando articular sus elementos y propiedades mediante la reconstrucción de significados asociados a ellos, permitiendo que adquieran un nuevo sentido para el estudiante, favoreciendo así su carácter funcional.

2.2. ANTECEDENTES DE INVESTIGACIÓN

A continuación se muestran algunos resultados de investigación, estudios realizados desde la Didáctica de la Matemática, que aportan a nuestra investigación.

Cordero (2006) declara que la graficación de funciones de R en R es una argumentación del Cálculo, por tal motivo, en su trabajo se debate sobre su funcionamiento y su forma desde una mirada socioepistemológica. En su artículo encontramos un aporte a esta investigación en torno a la importancia de la gráfica en la educación como un medio que soporta el desarrollo del razonamiento y la argumentación. Plantea que la modelación es un conocimiento y no una aplicación de la matemática (como es tratada en la educación actual), y que el uso de la gráfica es un tipo de modelación.

Micelli (2010) realiza una investigación desde una perspectiva socioespitemológica en torno a las figuras de análisis en geometría, entendiendo por ellas aquellos dibujos realizados a mano alzada por los estudiantes para resolver problemas geométricos, figuras que no poseen rigurosidad geométrica y vuelcan la información dada. El objetivo de Micelli es dar a conocer la naturaleza de las figuras de análisis tanto en el dME como en escenarios no académicos, con el fin de comprender e interpretar sus características, usos y funcionamientos. Señala que las figuras de análisis tienen varias funciones en la construcción del conocimiento matemático, entre ellas, funciones didácticas y sociales como la de apoyar la transmisión de ideas entre docentes y estudiantes o entre autores y lectores de los textos de matemática.

Balacheff (1999) nos advierte que la argumentación surge de manera natural del estudio de la interacción social entre los estudiantes. Además pone de manifiesto que un primer diagnóstico sería la naturaleza del contrato didáctico, donde es el docente quien garantiza la legitimidad y validez epistemológica de lo que se construye en la clase, negándole al alumno la posibilidad de acceder a la verdad y la prueba. De esta forma, Balacheff reafirma la importancia de los procesos de interacción social en la construcción de conocimiento, en los cuales surge de manera natural la argumentación para justificar o validar hipótesis que nacen de dichas interacciones entre los estudiantes, siendo coincidente con nuestra propuesta.

Chamorro (2007) declara que los niños "modelizan el espacio mediante la manipulación de formas geométricas" (p. 9) agregando que el trabajo con materiales debe estar muy presente en los primeros niveles, lo que constituye un referente de suma importancia, ya que dentro de nuestra propuesta se utiliza material concreto para que los estudiantes puedan adquirir las propiedades de los polígonos convexos. Agrega que el dominio de ciertas técnicas por parte de los alumnos del primer ciclo: plegado, recortado, ensamblado de piezas, de barras de mecano, etc., es necesario para poder realizar actividades posteriores de tipo práctico sobre las que fundamentar los conocimientos geométricos (matemáticas para la cabeza), por lo que creemos que la manipulación de materiales (matemáticas para las manos) es realmente necesaria. Sin esta experiencia sensible, cualquier intento de formalización es inútil y está destinado al fracaso.

2.3. UN RECORRIDO HISTÓRICO Y ASPECTOS EPISTEMOLÓGICOS DEL POLÍGONO

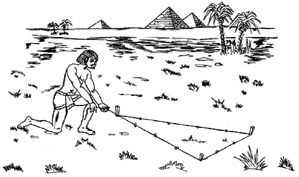
Según Boyer (1986), los orígenes de la geometría son incluso anteriores a los de la escritura, es por ello que toda afirmación que se haga al respecto deberá ser considerada una suposición. A los geómetras de Egipto se les llamaba "los tensadores de la cuerda" debido a que utilizaban las cuerdas tanto para bosquejar los planos de los templos como para reconstruir las fronteras borradas entre los terrenos (Ver Figura 1).

Figura 1. Tensadores de la cuerda egipcios

En Mesopotamia y Egipto surge el estudio de la figura geométrica y el descubrimiento de sus primeras propiedades basado en casos concretos. En Grecia, este estudio anterior se hace formal, consolidándose la Geometría como ciencia, pasando de enunciados de problemas particulares a enunciados generales y a una geometría axiomática en la que de unos pocos enunciados se deducen todos los demás mediante razonamiento general. Existen grandes diferencias en el desarrollo del estudio realizado por cada una de ellas en el sentido de la noción de demostración y el uso de las figuras geométricas, en específico los polígonos. Según los historiadores de la época, se cree que es muy probable que los griegos tomaran prestados elementos de la geometría elemental de Egipto como base para su desarrollo posterior, lo cual, para nuestra investigación, constituye un gran precedente en el sentido de que el estudio realizado por los egipcios basado en la búsqueda de regularidades entre figuras para formular propiedades y el inicio o paso previo a la compresión de la demostración rigurosa, podría ser visto desde los hallazgos de esta cultura y el previo uso de demostraciones no deductivas para poder comprender finalmente las propiedades generales y demostraciones formales.

En primera instancia, las figuras de polígonos que se estudian en Egipto son triángulos y cuadriláteros, las relaciones más exactas se hicieron a partir de figuras curvas, sin embargo, no se incluyó en el análisis debido a que el foco está puesto en las figuras de los polígonos. Luego, en Mesopotamia, se extiende al estudio de los polígonos regulares y en Grecia se hace un estudio general de la generalidad de la figura geométrica en dos dimensiones.

La búsqueda de relaciones deriva de la necesidad de conocer el área de la forma de los terrenos que quedaba después del desborde del río Nilo con el fin de pagar el tributo correspondiente al faraón. El uso de la figura geométrica es una modelación como práctica, pues a partir de él se desprenden las propiedades donde todo el análisis teórico parte del dibujo, del cual se puede llegar a formulación de carácter general. Los demás polígonos, creemos que no se estudiaron porque todos los descomponían para llegar a rectángulos, que debe ser, sin lugar a dudas, una figura muy estudiada por ellos. Los principios de la geometría egipcia son una colección de principios empíricamente descubiertos en relación con las longitudes, ángulos, áreas y volúmenes, que fueron desarrollados para satisfacer algunas necesidades en la agrimensura, la construcción, la astronomía y diversas artesanías.

Un punto de interés para nuestra investigación lo constituye el hecho de que se cree que los primeros griegos que desarrollaron la geometría como ciencia tomaron ideas de las culturas anteriores. Esto desde el punto de vista epistemológico constituye quizás un parámetro ausente en la reconstitución de sus objetos, pues de ser así, las prácticas desarrolladas por las civilizaciones prehelénicas nos pueden ayudar a reconstruir el desarrollo de la noción de polígono.

3. MARCO TEÓRICO

El marco teórico que sustenta nuestra investigación es la Teoría Socioepistemológica (TS) que concibe al proceso de enseñanza y aprendizaje de la matemática como una construcción social, considerando como foco a los fenómenos de producción y difusión del conocimiento matemático (Cordero, 2010). Cantoral (Cit. en Morales et al., 2012: 3) menciona que la TS es

Toma en consideración el papel que los escenarios históricos, culturales e institucionales desempeñan en la actividad humana, planteando un examen del conocimiento social, histórico y culturalmente situado, a la luz de la circunstancias de su construcción y difusión. Por otro lado, Arrieta et al. (2003) señalan que la socioepistemología reconoce y estudia científicamente las herramientas y los argumentos presentes en la construcción del conocimiento matemático.

3.1. DISCURSO MATEMÁTICO ESCOLAR (DME)

En la actualidad, el modelo de enseñanza de la matemática está centrado en los conceptos, a partir de ellos se entregan ejemplos, aplicaciones, etc. Cordero y Flores (2007) mencionan que el dME es la manifestación del conocimiento matemático normado por creencias de los actores del sistema didáctico de lo que es la enseñanza y lo que es la matemática. La crítica a este dME es que no ha logrado un nivel funcional del conocimiento matemático, sino más bien se ha dejado en un nivel utilitario, es decir, no ha podido atender a lo funcional porque no rinde cuentas de la construcción social del conocimiento matemático. Lo funcional tiene relación con un conocimiento incorporado orgánicamente en el humano que le transforma su realidad, en oposición al conocimiento utilitario. Lo anterior provoca que el aprendiz no logre hacer suyos los conocimientos ya que estos se le presentan de una manera acabada y con escasa posibilidad de que él logre construir o generarlos, de tal manera que frente a diversas situaciones pueda lograr articular y movilizar dichos conocimientos. Es así que uno de los objetivos de la TS es realizar un rediseño del discurso matemático escolar (RdME), para ello se deben crear marcos de referencia que permitan la resignificación del conocimiento matemático.

3.2. RESIGNIFICACIÓN

Entendemos la resignificación como la construcción del conocimiento mismo en la organización del grupo humano, normado por lo institucional, es decir, es el uso del conocimiento en la situación donde se debate entre su funcionamiento y forma acorde con lo que organizan los participantes (cf. Cordero 2006, 2010; Morales y Cordero, 2014). Un conocimiento matemático se resignifica en el momento en que los participantes desarrollen una matemática que sea funcional. Para lograr la resignificación se debe estudiar el uso del conocimiento, entendiéndolo como algo que se va organizando y cambiando, es decir, se va desarrollando en la situación o escenario que se enfrente, lo que va generando nuevos usos del conocimiento a través de su funcionamiento y forma, y por lo tanto nuevas resignificaciones (Morales et al., 2012).

3.3. MODELACIÓN

En la actualidad, la práctica de modelación se encuentra en pleno auge dentro de la Matemática Educativa, dado su rol en la construcción de conocimiento matemático; es por esto que las distintas concepciones que se tengan de ella juegan un rol relevante, debido a que no todas coinciden en la forma de entender cómo se construye el conocimiento matemático (Mena-Lorca, 2015 en prensa).

En nuestra investigación asumiremos a la modelación en el proceso de enseñanza y aprendizaje de las matemáticas como práctica. Suarez y Cordero (2008) señalan que la modelación debe ser considerada como una construcción teórica que un individuo realiza al enfrentar una tarea matemática en la que pone en juego sus conocimientos. La modelación como práctica es un aspecto que debe ser incluido en las situaciones de aprendizaje que se postulan para ser introducidas al aula, y creemos de gran relevancia potenciarla con el fin de que sea considerada en los planes de estudio como un conocimiento que debe ser enseñado.

3.4. ARGUMENTACIÓN GRÁFICA

Existen muchas investigaciones en relación al tema de la argumentación. Balacheff (1999) sostiene que en los procesos sociales surge espontáneamente el tema de la argumentación. Según Jean-Blaise Grize (Cit. en Balacheff, 1999: 2), "argumentar es sin duda una actividad con propósitos, pero es una actividad discursiva (donde el discurso sin embargo es concebido como una actividad social)". Por su parte, Duval (1999) considera como argumento todo aquello que se ofrece, o todo lo que es utilizado para justificar o para refutar una proposición. Con esto la argumentación sería un medio para convencer, sea a uno mismo o a los otros, pero nuestro enfoque es desde la perspectiva socioepistemológica, por lo que mencionamos el trabajo de Crespo, Farfan y Lezama (2010), quienes sostienen que los estudiantes no comprenden la necesidad de la demostración en el aula de matemática, apareciendo otras formas de argumentar no deductivas que son consideradas erróneas por el dME. Los autores sostienen que, por el contrario, estas argumentaciones deben ser analizarlas para saber cómo utilizarlas, conscientes de su utilidad y limitaciones. Concluyen que no se deben ignorar sino, por el contrario, se deben aprovechar a la hora de lograr construir nuevos conocimientos en nuestros estudiantes.

Hemos considerado los procesos argumentativos como parte de la construcción social de los conocimientos, como un saber en construcción que se reconstruye en la actividad del hombre y, por consiguiente, permite su resignificación. Con respecto al uso de la gráfica, consideramos a la gráfica no solo como la representación de una función en el sistema cartesiano, sino que también en relación a figuras que permiten desarrollar argumentaciones que facilitan la construcción de conocimiento matemático. En el dME hemos visto que la figura geométrica es considerada como una representación de un concepto, lo que hace alusión a volver a presentar lo que ya fue presentado, esto es, la figura geométrica es vista como una aplicación de conceptos abstractos como el triángulo, cuadrado, pentágono, etc. En esta investigación se plantea lo contrario, es decir, estudiar otros usos de la figura para la resignificación del conocimiento asociado a los polígonos, debido a que por medio de la situación planteada las figuras adquieren un rol argumentativo, lo que las posiciona en un estatus diferente, que no es reconocido en dME. Morales et al. (2012) señala que los profesores de matemática no promueven y, peor aún, no validan la argumentación gráfica ya que consideran a las figuras como representaciones de objetos matemáticos, privilegiando el uso de fórmulas, expresiones algebraicas. La figura, asociada a una situación de modelación-predicción, permite entender las propiedades matemáticas de los polígonos, donde el estudiante visualiza lo que ocurre cuando se analiza la variación de los elementos de los polígonos (número de lados, ángulos y sus medidas).

4. ASPECTOS METODOLÓGICOS

La metodología utilizada es de corte cualitativo debido a que se desea conocer y explicar los procesos de construcción de conocimiento matemático de polígonos en escenarios escolares en una situación de modelación, de esta forma se indaga específicamente en datos cualitativos tales como el tipo de argumentos que emergen del uso de la figura geométrica puesta a los participantes. Se ha optado por realizar un estudio de caso (Stake, 1998), específicamente un estudio de caso instrumental, que permite el estudio de la particularidad y de la complejidad de un caso singular en un contexto dado, debido a que se aplicó el instrumento a estudiantes de educación superior de una sola carrera y se desea una descripción detallada de la situación, de los comportamientos, de cómo interactúan los estudiantes, sus creencias y, principalmente, los argumentos matemáticos.

4.1. ESCENARIO Y ACTORES

Nuestro estudio tiene como objetivo ofrecer un diseño de situación para resignificar polígonos. La aplicación a estudiantes de pedagogía tenía dos sentidos, uno de ellos fue lograr poner en un nivel de funcionalidad sus conocimientos y el otro, que ellos pudieran explicar lo mismo a sus futuros estudiantes.

Por otra parte, creemos que es de suma importancia aportar marcos de referencia para mejorar los aprendizajes en geometría desde los niveles preescolares, y la mejor manera es realizarlo por medio de las futuras educadoras. De esta manera la unidad de estudio fue conformada por estudiantes de primer año de la carrera de Pedagogía en Educación Parvularia. No es relevante que estos ya tengan conceptos de geometría adquiridos en su educación escolar. En el estudio exploratorio se comprobó el efecto del dME, por lo tanto no tenían conocimientos funcionales de geometría.

4.2. RECOGIDA DE DATOS

La toma de datos fue de tres tipos: aplicación de un diseño de situación, observación y entrevista abierta. Las entrevistas fueron realizadas a todos los grupos constituidos en cada uno de los cursos. Las situaciones de aula (grabadas y digitadas como evidencia, autorizadas previamente con los informantes) fueron planteadas a los dos cursos de primer año (primer semestre) de Pedagogía en Educación Parvularia a quienes se les solicitó trabajar en grupos de no más de tres personas. El tiempo destinado a la realización del diseño de situación fue de aproximadamente 180 minutos. Para la implementación del diseño realizada a dos cursos de estudiantes de la unidad de estudio se precedió de la siguiente manera:

El investigador recoge los trabajos de cada grupo de estudiantes como datos. Se realizan entrevistas a los grupos de estudiantes con respecto a los hallazgos y obstáculos encontrados una vez terminada cada actividad. En cada momento concluido del diseño, se realiza una puesta en común de lo construido en la actividad y, posteriormente, se sigue con el momento siguiente, con los mismos pasos ya descritos.

4.3. EL DISEÑO

El diseño de situación⁴ propuesto está basado en la modelación como práctica, pone en juego el aspecto de la variación de los elementos de polígonos (medidas de lados y medida de ángulos). Su objetivo fundamental es la recolección de los argumentos gráficos que surgen del uso de las figuras geométricas con el fin de resignificar los polígonos a través de la variación y la búsqueda de regularidades tensionados por la variación de parámetros. Al dar un rol protagónico a la figura en nuestro modelo, se pretende explicar desde la teoría socioepistemológica lo que ocurre cuando la figura comienza a ser funcional para el estudiante y no solo es mirada como una representación del objeto polígono según el análisis del discurso matemático actual.

El diseño proporciona un contexto en el que la modelación y la predicción, consideradas como prácticas, hacen emerger herramientas, procedimientos y propiedades matemáticas que se evidencian cuando los estudiantes describen el comportamiento de un fenómeno utilizando el conocimiento funcional que tienen previamente. Construyen conjeturas a través de argumentos, utilizando en nuestro caso la figura geométrica y datos numéricos para validarlos.

Las actividades del diseño promueven el análisis de los elementos y propiedades que definen a los polígonos, para luego avanzar al reconocimiento de clases de figuras que presentan invariantes de acuerdo a la medida y número de lados y ángulos. Además se trabaja con la regularidad que presentan las figuras geométricas concretas para poder clasificarlas y llegar a la construcción de conocimiento en torno a los polígonos. El estudiante utiliza la lámina de polígonos para realizar las actividades, esta lámina presenta una colección de figuras geométricas, puntualmente solo polígonos (figuras geométricas cerradas) con distinto número de lados y ángulos, distinta medida de lados y ángulos con el fin de realizar clasificaciones. Las preguntas del diseño juegan un rol fundamental, pues están especialmente formuladas para recoger aquellos aspectos que nos interesan, que son la variación y la regularidad.

El diseño está compuesto por tres momentos y cada uno posee actividades en las que se pueden apreciar preguntas abiertas que pretenden aportar a la construcción de conocimiento, además de una lámina de figuras geométricas como apoyo visual.

Las nociones trabajadas en el diseño de situación, a través de sus momentos son:

5. RESULTADOS

5.1. MOMENTO I

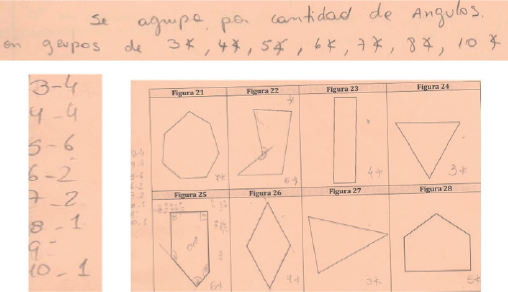
En la Actividad 1, letra a) todos los grupos lo hacen de acuerdo a número de lados, de vértices y/o ángulos. Dentro de los argumentos mencionados, destacamos algunas conclusiones como: clasificar de acuerdo a cantidad de ángulos es igual a clasificar de acuerdo a cantidad de lados (ver Imagen 1).

Imagen 1. G1 asocia las figuras por cantidad de ángulos, luego etiqueta las
figuras y realiza una tabla resumen

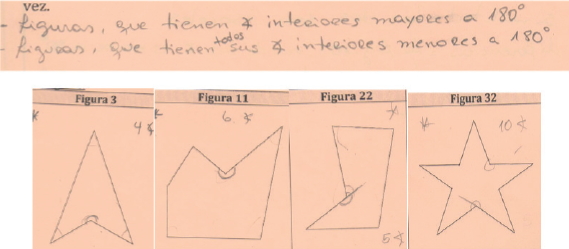
En la letra b) todos los grupos identifican que hay polígonos cóncavos y convexos, dos grupos responden por forma y el otro comprueba dicha relación, midiendo y marcando los ángulos. El G1 clasifica en figuras que tienen al menos un ángulo interior mayor a 180°, dando mayor precisión en el lenguaje geométrico empleado, y figuras que tienen todos sus ángulos interiores menores a 180°. Lo anterior lo justifican por medio de la medición (Ver Imagen 2).

Imagen 2. Respuesta G1

5.2. MOMENTO II

En la actividad 1, letra a) y b) todos los grupos miden figuras y descubren que sus ángulos suman 180° y 540° respectivamente, miden más de una figura para comprobar sus resultados.

Luego, en la letra c) un integrante de un grupo se da cuenta que hay una relación y la comienza a buscar, el resto de los grupos dibujan una figura de 9 lados que ya no está en la lámina y miden sus ángulos. En la letra d) un grupo, el que se percató que había una relación, busca la regularidad y escribe como la obtuvo (Ver Imágenes 3 y 4).

Imagen 3 a. Respuesta G1

Imagen 3 b. Respuesta G2

Imagen 4 a. Construye tabla de datos para
estudiar las regularidades observadas

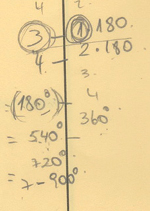
Imagen 4 b. G2 mide una figura construida

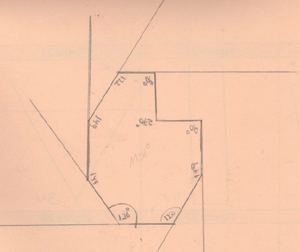
En la actividad 2, letra a), todos los grupos comienzan a buscar regularidades con los datos que tienen, algunos piensan en dibujar, pero es una tarea imposible. Cuando comienzan a buscar las regularidades, realizan tablas de número de lados versus suma de sus medidas de ángulos interiores, encontrando que había una diferencia de 180° a medida que aumentaba en un lado la figura. Se observa que no miden solo una figura de cada tipo, sino que prueban con más de una. En los grupos que encontraron la relación exacta fue (116-2) x180°. Esta pregunta les hace surgir la inquietud de la existencia de algún algoritmo más sencillo para encontrar el resultado en lugar de dibujar o realizar una tabla que contemple desde 3 a 116 lados, con lo que recurren a la predicción.

Posteriormente, en la letra b) lo que se necesita es modelar una relación general, para la pregunta anterior no era necesario modelar, ahora deben ir a la búsqueda de la generalidad. Algunas respuestas: 1. Primero piensan en 180 x número de lados, y al comprobar se dan cuenta que no sirve, luego: 2. Piensan en cantidad de lados - 2 x 180°, pero no se dan cuenta de que es necesario poner un paréntesis, finalmente dos grupos llegan a (n-2) x180°, luego de una conversación entre ellos. 3. En otro grupo una alumna llega a la relación "180° x número de lados -360°" (Ver Imagen 5 y 6).

Imagen 5. G3 muestra su tabla de datos

Imagen 6. G2 da cuenta de la variación

5.3. MOMENTO III

En la actividad 2, pregunta 1, comienzan a analizar las figuras más a fondo y estudian las características de cada una de ellas. Encuentran una relación entre las medidas de los lados relacionado con la fórmula de la suma de los ángulos anteriores que obtuvieron en el momento III. En la pregunta 2 se trata un asunto que ya solucionaron en la primera parte de esta actividad y solo lo escriben (Ver imagen 7).

Imagen 7. Respuesta G1

6. CONCLUSIONES

Nuestro objetivo fue dar a conocer la importancia en la construcción y/o resignificación de conocimiento matemático, de las argumentaciones gráficas que emergen del uso que se dio a la figura geométrica en una situación en que se ha intencionalizado la aparición de la práctica de modelación por medio de la variación de los elementos de figuras geométricas. Es por esto que la evidencia encontrada nos permite concluir que la argumentación gráfica debe ser ubicada en un estatus privilegiado en la matemática que se enseña, ya que nos dio cuenta de ser una herramienta muy útil permitiendo poner los conocimientos en juego a un nivel funcional.

La argumentación gráfica, como hilo conductor en un proceso de modelación, provoca que surjan argumentos, en este caso nacen de la toma datos y búsqueda de relaciones que derivan de la experimentación con la figura, por lo que este conocimiento comienza a ser funcional y a partir de ese momento, es capaz de movilizarlo a otro tipo de situaciones como se observó en el momento III. Los argumentos que emergieron de la situación permitieron que el conocimiento en cuestión adquiera un nuevo significado para los estudiantes, debido a que en la búsqueda de relaciones comienzan a poner atención en aspectos que el discurso matemático escolar le entrega vía formulas, dándoles la posibilidad de validar por ellos mismos la legitimidad del conocimiento que se pone a su disposición.

Se evidencia que aprende a identificar relaciones en la figura y a reconocer patrones de comportamientos entre ellas para el establecimiento de propiedades como la de la suma de sus ángulos interiores, en este caso particular, y a extrapolarlo a otro tipo de figuras especiales como las regulares. Todo esto nos permite mencionar que en una situación específica el rol que adquiere la argumentación gráfica permite el desarrollo de modelos geométricos, debido a que las propiedades, en este caso del polígono, adquieren otro significado y sentido.

Desde el punto de vista cognitivo, la figura es un soporte intuitivo indudable, representa una herramienta de análisis que proporciona información visual de las propiedades de los polígonos. Es por eso que se debe potenciar el trabajo con ellas, en esta investigación se le dio nuevos usos, no solo para la representación de un enunciado, sino una herramienta para modelar y predecir, la figura en sí fue un argumento que permitió la resignificación del conocimiento que ayuda a las estudiantes a encontrar importantes relaciones y propiedades. La figura deja de ser un simple dibujo y comienza a ser un modelo; una figura geométrica que está compuesta de lados, vértices y ángulos.

NOTAS

¹ La investigación hace referencia a "la educadora de párvulos" para referirnos tanto a educadoras como a educadores de párvulos, atendiendo a la composición mayoritariamente femenina de estas profesionales y su estudiantes.

² En Cordero y Flores (2007) El discurso matemático escolar es la manifestación del conocimiento matemático normado por creencias de los actores del sistema didáctico de lo que es la enseñanza y lo que es la matemática.

³ Entendemos la resignificación como la construcción del conocimiento mismo en la organización del grupo humano, normado por lo institucional. Ver más detalle en el apartado 3.

⁴ Ver Anexo 1.

⁵ No fue presentada la "lamina de figuras" en este anexo

REFERENCIAS BIBLIOGRÁFICAS

Arrieta, J. (2003). Las prácticas de modelación como proceso de matematización en el aula (Tesis doctoral no publicada). Centro de Investigación y de Estudios Avanzados del IPN, México.

Arrieta, J., Buendía, G., Ferrari, M., Martínez, G., & Suárez, L. (2003). Las prácticas sociales como generadoras del conocimiento matemático. Acta Latinoamericana de Matemática Educativa, 17, 418-422.

Balachef, N. (1999). ¿Es la argumentación un obstáculo? Invitación a un debate. Prueba, International Newsletter on the Teaching and Learning of Mathematical Proof. Grenoble France: Laboratorie Leibniz.

Ballestero, E., & Gamboa, R. (2010). La enseñanza y aprendizaje de la geometría en secundaria, la perspectiva de los estudiantes. Revista Electrónica Educare, 14(2), 125-142.

Boyer, C. (1986). Historia de la matemática. España: Alianza editorial.

Chamorro, M. (2007). Matemáticas para la cabeza y las manos: La enseñanza de la Geometría en la Educación Primaria. Revista Quehacer Educativo, 83.

Cordero, F. (2006). La modellazione e la rappresentazione grafica nell'insegnamento-apprendimento della matemática. La Matemática e la sua Didattica, 20(1), 59-79.

Cordero, F., Cen, C., & Suárez, L. (2010) Los funcionamientos y formas de las gráficas en los libros de texto: Una práctica institucional en el bachillerato. Revista Latinoamericana de Investigación en Matemática Educativa, 13(2), 187-214.

Cordero, F., & Flores, R. (2007). El uso de las gráficas en el discurso matemático escolar. Un estudio socioepistemológico en el nivel básico a través de los libros de texto. Revista Latinoamericana de Investigación en Matemática Educativa, 10(1), 7-38.

Crespo, C., Farfán, R., & Lezama, J. (2010). Argumentaciones y demostraciones: Una visión de la influencia de los escenarios socioculturales. Revista Latinoamericana de Investigación en Matemática Educativa, 13(3), 129-158.

Duval, R. (1999). Algunas cuestiones relativas a la argumentación. International Newsletter on the teaching and learning of mathematical Proof. Francia: IUFM de Lille.

Godino, J., Batanero, C., Cid, E., Font, V., Ruiz, F., & Roa, R. (2004). Matemáticas para maestros. Granada: Departamento de Didáctica de la Matemática. Universidad de Granada.

Mena-Lorca, J. (en prensa). Modelación matemática y la construcción del conocimiento matemático. Investigaciones Latinoamericanas en Modelación Matemática Educativa.

Micelli, M. (2010). Las figuras de análisis en geometría. Su utilización en el aula de matemática (Tesis magíster no publicada). Centro de Investigación en Ciencia Aplicada y Tecnología. México.

Mineduc. (2001). Bases Curriculares Educación Parvularia. Santiago, Chile: Autor. Recuperado desde: http://www.mineduc.cl/usuarios/parvularia/doc/201308281105060.bases_curriculares_educacion_parvularia.pdf.

Mineduc. (2004). Chile y el aprendizaje de matemáticas y ciencias según TIMSS. Unidad de Currículum y Evaluación, SIMCE. Santiago, Chile: Autor. Recuperado desde www.oei.es/quipu/chile/pruebaTIMSS2003.pdf

Mineduc. (2008). Programa de estudio Primer Nivel de Transición. Santiago, Chile: Autor. Recuperado desde: http://curriculumenlineamineduc.cl/sphider/search.php?query=&t_busca=1&results=&search=1&dis=0&category=10

Mineduc. (2012a). Estándares Orientadores para Carreras de Educación Parvularia. Estándares Pedagógicos y Disciplinarios. Santiago, Chile: Autor. Recuperado desde: http://www.mineduc.cl/usuarios/cpeip/doc/201205111816290.LibroEstandaresOrientadoresCarrerasEducaciOnParvulariaconcarta.pdf.

Mineduc. (2012b). Bases Curriculares Educación Básica. Santiago, Chile: Autor. Recuperado desde: http://www.curriculumenlineamineduc.cl/605/w3-article-14598.html

Morales, A., & Cordero, F. (2014). La Graficación-modelación y la Serie de Taylor. Una socioepistemología del cálculo. Revista Latinoamericana de Investigación en Matemática Educativa, 17(3), 319-345. doi: 10.12802/relime.13.1733

Morales, A., Mena, J., Vera, F., & Rivera, R. (2012). El rol del tiempo en un proceso de modelación utilizando videos de experimentos físicos. Enseñanza de las Ciencias. Revista de Investigación y experiencias didácticas, 30(3), 237-256. doi: http://dx.doi.org/10.5565/rev/ec/v30n3.694

Stake, R. (1998). Investigación con estudio de casos. Madrid: Ediciones Morata, S. L.

Suárez, L., & Cordero, F. (2008). Elementos teóricos para estudiar el uso de las gráficas en la modelación del cambio y de la variación en un ambiente tecnológico. Revista Electrónica de Investigación en Educación en Ciencias, 3(1), 51-58.

ANEXO 1